
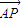 ∥
∥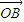 ,
,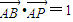 .
.
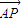 ∥
∥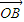 ,
,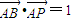 ,可得
,可得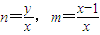 ,利用点B在单位圆上,即可点P的轨迹E的方程;
,利用点B在单位圆上,即可点P的轨迹E的方程;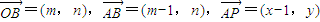
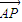 ∥
∥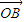 ,
,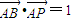 .
.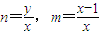
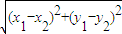 =2(1+m2)≥2(当且仅当m=0时取等号)
=2(1+m2)≥2(当且仅当m=0时取等号)

科目:高中数学 来源: 题型:
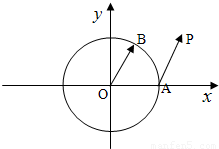
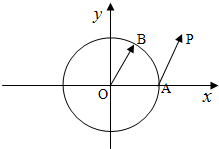 已知单位圆⊙O:x2+y2=1,A(1,0),B是圆上的动点,
已知单位圆⊙O:x2+y2=1,A(1,0),B是圆上的动点,| AP |
| OB |
| AB |
| AP |
查看答案和解析>>
科目:高中数学 来源:江苏省南通四县市合作编写的2007高考数学模拟试题集(三) 题型:022
已知O为坐标原点,点P(x,y)在单位圆x2+y2=1上,点Q(2cosθ,2sinθ)满足![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com