
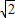 .
.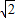 ,利用点到直线的距离公式列出关于a的方程,求出方程的解得到a的值,进而确定出圆C的方程;
,利用点到直线的距离公式列出关于a的方程,求出方程的解得到a的值,进而确定出圆C的方程;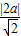 ,又d=
,又d=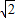 ,
,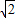 ,圆的半径r=1,
,圆的半径r=1,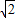 +1,最小值为d-r=
+1,最小值为d-r=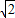 -1,
-1,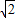 -1)2,(
-1)2,(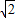 +1)2],即[3-2
+1)2],即[3-2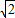 ,3+2
,3+2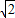 ].
].

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
| 2 |
| x |
| m |
| y |
| n |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
| m |
| y |
| n |
| mn+2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源:2014届山东省济宁市高二上学期期末文科数学试卷(解析版) 题型:解答题
已知圆C与两坐标轴都相切,圆心C到直线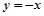 的距离等于
的距离等于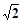 .
.
(1)求圆C的方程.
(2)若直线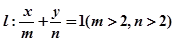 与圆C相切,求证:
与圆C相切,求证: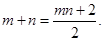
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高三3月月考数学试卷(解析版) 题型:解答题
已知圆C与两坐标轴都相切,圆心C到直线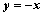 的距离等于
的距离等于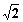 .
.
(1)求圆C的方程.
(2)若直线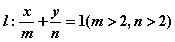 与圆C相切,求
与圆C相切,求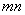 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com