
| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
分析 根据条件便可求出$|\overrightarrow{AB}|,|\overrightarrow{DC}|$,以及$\overrightarrow{AB}•\overrightarrow{DC}$的值,从而可求出$cos<\overrightarrow{AB},\overrightarrow{DC}>$的值,进而得出异面直线AB与DC所成角θ的大小.
解答 解:$|\overrightarrow{AB}|=\sqrt{20}=2\sqrt{5}$,$|\overrightarrow{DC}|=\sqrt{10}$,$\overrightarrow{AB}•\overrightarrow{DC}=10$;
∴$cos<\overrightarrow{AB},\overrightarrow{DC}>=\frac{10}{2\sqrt{5}×\sqrt{10}}=\frac{\sqrt{2}}{2}$;
∴$<\overrightarrow{AB},\overrightarrow{DC}>=45°$;
∴异面直线AB与DC所成角θ的大小为45°.
故选A.
点评 考查根据向量坐标求向量长度的公式,向量数量积的坐标运算,以及向量夹角余弦的坐标公式.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
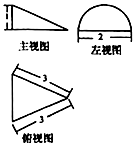
| A. | $\frac{\sqrt{2}}{3}$π | B. | 2$\sqrt{2}$+2π | C. | $\frac{2\sqrt{2}}{3}$π | D. | 2$\sqrt{2}$+$\frac{3}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数,在(-∞,0)上是减函数 | B. | 奇函数,在(-∞,0)上是增函数 | ||
| C. | 偶函数,在(-∞,0)上是减函数 | D. | 偶函数,在(-∞,0)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
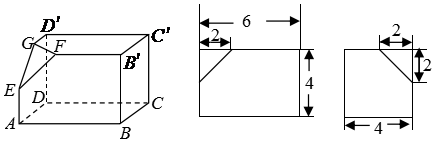
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com