
分析 (1)利用有理数指数幂性质、运算法则求解.
(2)利用对数性质、运算法则求解.
解答 解:(1)$\frac{{5{x^{-\frac{2}{3}}}{y^{\frac{1}{2}}}}}{{({-\frac{1}{4}{x^{-1}}{y^{\frac{1}{2}}}})({-\frac{5}{6}{x^{\frac{1}{2}}}{y^{-\frac{1}{6}}}})}}$
=$5×(-4)×(-\frac{6}{5})$×${x}^{-\frac{2}{3}+1-\frac{1}{2}}$×${y}^{\frac{1}{2}-\frac{1}{2}+\frac{1}{6}}$
=24${x}^{-\frac{1}{6}}{y}^{\frac{1}{6}}$.
(2)∵log53=a,log52=b,
∴${log_{25}}12=\frac{{{{log}_5}12}}{{{{log}_5}25}}=\frac{{{{log}_5}3+2{{log}_5}2}}{2}=\frac{a+2b}{2}$.
点评 本题考查指数式、对数式化简求值,是基础题,解题时要认真审题,注意指数、对数性质、运算法则的合理运用.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
 如图,某几何体的三视图中,正视图和侧视图都是半径为$\sqrt{3}$的半圆和相同的正三角形,其中三角形的上顶点是半圆的中点,底边在直径上,则它的表面积是( )
如图,某几何体的三视图中,正视图和侧视图都是半径为$\sqrt{3}$的半圆和相同的正三角形,其中三角形的上顶点是半圆的中点,底边在直径上,则它的表面积是( )| A. | 6π | B. | 8π | C. | 10π | D. | 11π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
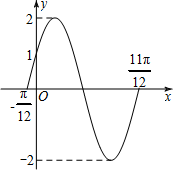 若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分图象如图所示.
若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b?α,则a∥b | B. | 若a∥b,a⊥α,则b⊥α | C. | 若a∥b,a∥α,则b∥α | D. | 若a⊥b,a⊥α,则b∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11π | B. | 20π | C. | 23π | D. | 35π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
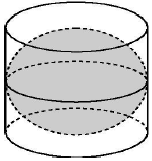 如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现.经计算球的体积等于圆柱体积的$\frac{2}{3}$倍.
如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现.经计算球的体积等于圆柱体积的$\frac{2}{3}$倍.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-1≤k≤\frac{5}{4}$ | B. | $-\frac{5}{4}≤k≤1$ | C. | $0≤k≤\frac{5}{4}$ | D. | $-\frac{5}{4}≤k≤0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com