
【题目】设正项数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]()
(1)求证:数列![]() 是等差数列,并求其通项公式
是等差数列,并求其通项公式
(2)设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,若
,若![]() 对任意
对任意![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为 (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我校高2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况,对全年级2000名高三学生进行了问卷调查,统计结果如下表:
校区 | 愿意参加 | 不愿意参加 |
重庆一中本部校区 | 220 | 980 |
重庆一中大学城校区 | 80 | 720 |
(1)若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人,则大学城校区应抽取几人;
(2)现对愿意参加自主招生的同学组织摸底考试,考试题共有5道题,每题20分,对于这5道题,考生“如花姐”完全会答的有3题,不完全会的有2道,不完全会的每道题她得分![]() 的概率满足:
的概率满足:![]() ,假设解答各题之间没有影响,
,假设解答各题之间没有影响,
①对于一道不完全会的题,求“如花姐”得分的均值![]() ;
;
②试求“如花姐”在本次摸底考试中总得分的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(5分)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第五节的容积为( )
A. 1升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角梯形ABCD如图(1)所示,其中![]() ,
,![]() ,过点B作
,过点B作![]() ,垂足为M,得到面积为4的正方形ABMD,现沿BM进行翻折,得到如图(2)所示的四棱柱C-ABMD.
,垂足为M,得到面积为4的正方形ABMD,现沿BM进行翻折,得到如图(2)所示的四棱柱C-ABMD.
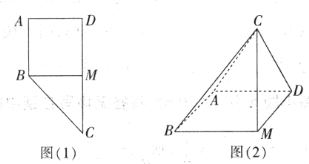
(1)求证:平面![]() 平面CDM;
平面CDM;
(2)若![]() ,平面CBM与平面CAD所成锐二面角的余弦值为
,平面CBM与平面CAD所成锐二面角的余弦值为![]() ,求CM的长.
,求CM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解贵州省某州2020届高三理科生的化学成绩的情况,该州教育局组织高三理科生进行了摸底考试,现从参加考试的学生中随机抽取了100名理科生,,将他们的化学成绩(满分为100分)分为![]()
![]()
![]()
![]()
![]()
![]() 6组,得到如图所示的频率分布直方图.
6组,得到如图所示的频率分布直方图.
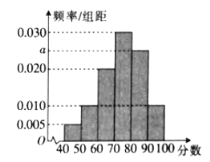
(1)求a的值;
(2)记A表示事件“从参加考试的所有理科生中随机抽取一名学生,该学生的化学成绩不低于70分”,试估计事件A发生的概率;
(3)在抽取的100名理科生中,采用分层抽样的方法从成绩在![]() 内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在
内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在![]() 内的人数为X,求X的分布列与数学期望.
内的人数为X,求X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com