
【题目】已知函数f(x)=lnx,g(x)= ![]() ax2+bx,a≠0.
ax2+bx,a≠0.
(Ⅰ)若b=2,且h(x)=f(x)﹣g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1 , C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.
【答案】解:(Ⅰ)b=2时,h(x)=lnx﹣ ![]() ax2﹣2x,
ax2﹣2x,
则h′(x)= ![]() ﹣ax﹣2=﹣
﹣ax﹣2=﹣ ![]() .
.
因为函数h(x)存在单调递减区间,所以h'(x)<0有解.
又因为x>0时,则ax2+2x﹣1>0有x>0的解.
①当a>0时,y=ax2+2x﹣1为开口向上的抛物线,ax2+2x﹣1>0总有x>0的解;
②当a<0时,y=ax2+2x﹣1为开口向下的抛物线,而ax2+2x﹣1>0总有x>0的解;
则△=4+4a≥0,且方程ax2+2x﹣1=0至少有一正根.此时,﹣1<a<0.
综上所述,a的取值范围为(﹣1,0)∪(0,+∞).
(Ⅱ)设点P、Q的坐标分别是(x1 , y1),(x2 , y2),0<x1<x2 .
则点M、N的横坐标为x= ![]() ,
,
C1在点M处的切线斜率为k1= ![]() ,x=
,x= ![]() ,k1=
,k1= ![]() ,
,
C2在点N处的切线斜率为k2=ax+b,x= ![]() ,k2=
,k2= ![]() +b.
+b.
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2 .
即 ![]() =
= ![]() +b,
+b,
则 ![]()
= ![]() (x22﹣x12)+b(x2﹣x1)
(x22﹣x12)+b(x2﹣x1)
= ![]() (x22+bx2)﹣(
(x22+bx2)﹣( ![]() +bx1)
+bx1)
=y2﹣y1
=lnx2﹣lnx1 .
所以 ![]() =
= 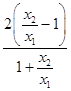 .设t=
.设t= ![]() ,则lnt=
,则lnt= ![]() ,t>1①
,t>1①
令r(t)=lnt﹣ ![]() ,t>1.则r′t=
,t>1.则r′t= ![]() ﹣
﹣ ![]() =
= 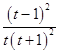 .
.
因为t>1时,r'(t)>0,所以r(t)在[1,+∞)上单调递增.故r(t)>r(1)=0.
则lnt> ![]() .这与①矛盾,假设不成立.
.这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行
【解析】(Ⅰ)先求函数h(x)的解析式,因为函数h(x)存在单调递减区间,所以h'(x)<0有解,求出a的取值范围;(Ⅱ)先利用导数分别表示出函数在C1在点M处的切线与C2在点N处的切线,结合过线段PQ的中点作x轴的垂线分别交C1 , C2于点M、N,建立关系式,通过反证法进行证明即可.
【考点精析】认真审题,首先需要了解函数单调性的性质(函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集).


科目:高中数学 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
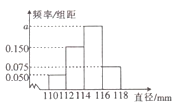
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位需要从甲、乙两人中选拔一人参加新岗位培训,特别组织了5个专项的考试,成绩统计如下:
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 | 81 | 82 | 79 | 96 | 87 |
乙的成绩 | 94 | 76 | 80 | 90 | 85 |
(1)根据有关统计知识,回答问题:若从甲、乙2人中选出1人参加新岗位培训,你认为选谁合适,请说明理由;
(2)根据有关概率知识,解答以下问题:
从甲、乙两人的成绩中各随机抽取一个,设抽到甲的成绩为![]() ,抽到乙的成绩为
,抽到乙的成绩为![]() ,用
,用![]() 表示满足条件
表示满足条件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年某学科能力测试共有12万考生参加,成绩采用15级分,测试成绩分布图如图,试估计成绩高于11级分的人数为 ( )

A. 8 000 B. 10 000 C. 20 000 D. 60 000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是甲、乙两名运动员某赛季一些场次得分的茎叶图,据图可知以下说法正确的是 _____.(填序号)

①甲运动员的成绩好于乙运动员;②乙运动员的成绩好于甲运动员;
③甲、乙两名运动员的成绩没有明显的差异;④甲运动员的最低得分为0分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P-ABC中,PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD![]() 平面PAB
平面PAB
(1)求证:AB![]() 平面PCB
平面PCB
(2)求异面直线AP与BC所成角的大小
(3)求二面角C-PA-B 的大小的余弦值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com