练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    随机询问100名性别不同的大学生是否爱好踢毽子运动，得到如下的列联表：

     
    		男
    		女
    		总计
    爱好
    		10
    		40
    		50
    不爱好
    		20
    		30
    		50
    总计
    		30
    		70
    		100
    附表：
    P(K2≥k0)
    		0.10
    		0.05
    		0.025
    k0
    		2.706
    		3.841
    		5.024
    经计算，统计量K2＝4.762，参照附表，得到的正确结论是(　　)．
    A．在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关”
    B．在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关”
    C．有97.5%以上的把握认为“爱好该项运动与性别有关”
    D．有97.5%以上的把握认为“爱好该项运动与性别无关”

    A

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    一组数据的方差是s2，将这组数据中的每一个数据都乘以2，所得到的一组数据的方差是

    A．2s2B．4s2C．8s2D．16s2

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某班有男生36人，女生18人，用分层抽样的方法从该班全体学生中抽取一个容量为9的样本，则抽取的女生人数为（    ）

    A．6 B．4 C．3 D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知样本
    7,10,14,8,7,12,11,10,8,10,13,10,8,11,8,9,12,9,13,20,那么这组数据落在8.5～11.5的频率为(　　)

    A．0.5 B．0.4 C．0.3 D．0.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，x1，x2分别表示甲、乙两名运动员这项测试成绩的平均数，s1，s2分别表示甲、乙两名运动员这项测试成绩的标准差，则有(　　)

    A．x1>x2，s1<s2B．x1＝x2，s1>s2
    C．x1＝x2，s1＝s2D．x1＝x2，s1<s2

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    根据一组样本数据(x1，y1)，(x2，y2)，…，(xn，yn)的散点图分析存在线性相关关系，求得其回归方程＝0.85x－85.7，则在样本点(165，57)处的残差为(　　)

    A．54.55B．2.45C．3.45D．111.55

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，在下面的抽样方法中，最合理的抽样方法是(　　)

    A．简单随机抽样　　　　　 B．按性别分层抽样
    C．按学段分层抽样 D．系统抽样

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知x与y之间的几组数据如下表：

    x
    		1
    		2
    		3
    		4
    		5
    		6
    y
    		0
    		2
    		1
    		3
    		3
    		4
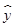    假设根据上表数据所得线性回归直线方程 ＝ x＋ ，若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y＝b′x＋a′，则以下结论正确的是(　　)．
    A.>b′， >a′  B.>b′， <a′
    C. <b′， >a′  D.<b′， <a′

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某地区教育主管部门为了对该地区模拟考试成绩进行分析，抽取了总成绩介于350分到650分之间的10 000名学生成绩，并根据这10 000名学生的总成绩画了样本的频率分布直方图(如图所示)，则总成绩在[400,500)内共有(　　)．

    A．5000人 B．4500人 C．3250人 D．2500人

    查看答案和解析>>

    同步练习册答案