
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)求函数![]() 单调区间;
单调区间;
(2)当![]() 时,
时,
①求函数![]() 在
在![]() 上的值域;
上的值域;
②求证:![]() ,其中
,其中![]() ,
,![]() .(参考数据
.(参考数据![]() )
)
【答案】(1)见解析;(2) ①![]() ;②见解析.
;②见解析.
【解析】试题分析: (1)先求导数,再研究导函数符号:当![]() 时,恒为正;当
时,恒为正;当![]() 时,有正有负,根据符号规律确定单调区间,(2)①易得函数
时,有正有负,根据符号规律确定单调区间,(2)①易得函数![]() 在
在![]() 单调性:先减后增,故在极小值点处取最小值,最大值为两端点值的较大值,②由所证不等式的结构知,先研究数列求和:令
单调性:先减后增,故在极小值点处取最小值,最大值为两端点值的较大值,②由所证不等式的结构知,先研究数列求和:令![]() ,可得
,可得![]() ,再比较对应项大小:
,再比较对应项大小:![]() ,这样转化为证明不等式
,这样转化为证明不等式![]() ,利用导数研究函数
,利用导数研究函数![]() 单调性,即可证得.
单调性,即可证得.
试题解析:(1)∵![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增;
单调递增;
②当![]() 时,令
时,令![]() ,得
,得![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增.
单调递增.
(2)![]() 时,
时,![]() .
.
①由![]() ,令
,令![]() ,
,
∴![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,且由
单调递增,且由![]() ,
,![]() ,
,
∴值域为![]() .
.
②由![]() ,设
,设![]() 为
为![]() 前
前![]() 项和,
项和,![]() ,
,
则![]() ,
,
设![]() ,
,![]() ,
,
![]() 在
在![]() 单调递减,
单调递减,![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() 时,
时,![]() ,
,
∴![]() ,故原不等式成立.
,故原不等式成立.


科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民全月工资所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额。此项税款按下表分段累计计算:
全月应纳税所得额 | 税率(%) |
不超过1500元的部分 | 3 |
超过1500元至4500元的部分 | 10 |
超过4500元至9000元的部分 | 20 |
(1)某人10月份应交此项税款为350元,则他10月份的工资收入是多少?
(2)假设某人的月收入为![]() 元,
元, ![]() ,记他应纳税为
,记他应纳税为![]() 元,求
元,求![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,求数列
,求数列![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _________,
_________, ![]() __________,
__________, ![]() _________.
_________.
猜想: ![]() _______.
_______.
然后用数学归纳法证明.证明过程如下:
①当![]() 时,________________,猜想成立
时,________________,猜想成立
②假设![]() (
(![]() N*)时,猜想成立,即
N*)时,猜想成立,即![]() _______.
_______.
那么,当![]() 时,由已知
时,由已知![]() ,得
,得![]() _________.
_________.
又![]() ,两式相减并化简,得
,两式相减并化简,得![]() _____________(用含
_____________(用含![]() 的代数式表示).
的代数式表示).
所以,当![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何![]() N*都成立.
N*都成立.
思路2:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _____________.
_____________.
由已知![]() ,写出
,写出![]() 与
与![]() 的关系式:
的关系式: ![]() _____________________,
_____________________,
两式相减,得![]() 与
与![]() 的递推关系式:
的递推关系式: ![]() ____________________.
____________________.
整理: ![]() ____________.
____________.
发现:数列![]() 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.
得出:数列![]() 的通项公式
的通项公式![]() ____,进而得到
____,进而得到![]() ____________.
____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)求f(2)与f![]() , f(3)与f
, f(3)与f![]() ;
;
(2)由(1)中求得结果,你能发现f(x)与f![]() 有什么关系?并证明你的发现;
有什么关系?并证明你的发现;
(3)求f(1)+f(2)+f(3)+…+f(2013)+f![]() +f
+f![]() +…+f
+…+f![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程![]() 关于时间
关于时间![]() 的函数关系式分别为
的函数关系式分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,有以下结论:
,有以下结论:
①当![]() 时,甲走在最前面;
时,甲走在最前面;
②当![]() 时,乙走在最前面;
时,乙走在最前面;
③当![]() 时,丁走在最前面,当
时,丁走在最前面,当![]() 时,丁走在最后面;
时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() ,
, ![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ,
, ![]() )分别交
)分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点,当
两点,当![]() 取何值时,
取何值时, ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
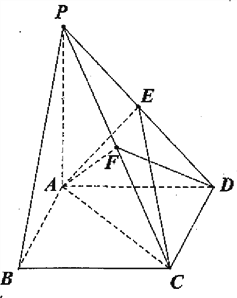
【题目】如图,四棱锥P—ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形,![]() ,求二面角C—AF—D大小.
,求二面角C—AF—D大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com