解:(1)设y=f(x)与y=g(x)(x>0)在公共点(x
0,y
0)处的切线相同.
f′(x)=x+2a,g′(x)=
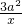
.
由题意知f(x
0)=g(x
0),f′(x
0)=g′(x
0)
即
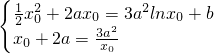
,
解得x
0=a或x
0=-3a(舍去),
b=
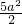
-3a
2lna(a>0)
(2)b'(a)=5a-6alna-3a=2a(1-3lna).
令b'(a)=0,则
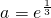
,当a变化时,b'(a)及b(a)的变化情况如下表:
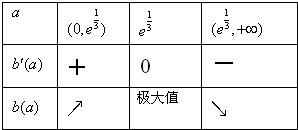
所以,
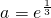
时,b(a)有最大值
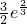
.
(3)h(x)=

x
2+3a
2lnx-6x,h′(x)=x+
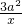
-6
要使h(x)在(0,4)上单调,
须h′(x)=x+
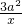
-6≤0或h′(x)=x+
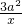
-6≥0在(0,4)上恒成立.
h′(x)=x+
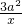
-6≤0在(0,4)上恒成立
?3a
2≤-x
2+6x在(0,4)上恒成立.
而-x
2+6x>0,且-x
2+6x可为足够小的正数,必有a=0
或h′(x)=x+
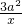
-6≥0在(0,4)上恒成立
?3a
2≥(-x
2+6x)
max=9,得a≥

或a≤-

.
综上,所求a的取值范围为a≥

或a≤-

或a=0.
分析:(1)设公共点(x
0,y
0),根据题意得到,f(x
0)=g(x
0),f′(x
0)=g′(x
0),解出b关于a的函数关系式;
(2)令b'(a)=0,得a=
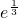
,经过判断当a=
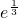
时,b(a)为极大值,即b的最大值;
(3)根据已知h(x)为单调函数,则h′(x)≥0或h′(x)≤0,解出a的取值范围即可.
点评:本题主要考查函数的单调性、极值、最值等函数的基础知识,是一道关于函数的综合题,应熟练掌握其求解的方法步骤.

 x2+2ax,g(x)=3a2lnx+b.其中a,b∈R.
x2+2ax,g(x)=3a2lnx+b.其中a,b∈R.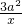 .
.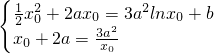 ,
,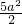 -3a2lna(a>0)
-3a2lna(a>0)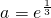 ,当a变化时,b'(a)及b(a)的变化情况如下表:
,当a变化时,b'(a)及b(a)的变化情况如下表:
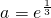 时,b(a)有最大值
时,b(a)有最大值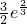 .
. x2+3a2lnx-6x,h′(x)=x+
x2+3a2lnx-6x,h′(x)=x+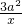 -6
-6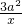 -6≤0或h′(x)=x+
-6≤0或h′(x)=x+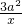 -6≥0在(0,4)上恒成立.
-6≥0在(0,4)上恒成立.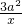 -6≤0在(0,4)上恒成立
-6≤0在(0,4)上恒成立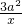 -6≥0在(0,4)上恒成立
-6≥0在(0,4)上恒成立 或a≤-
或a≤- .
. 或a≤-
或a≤- 或a=0.
或a=0.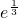 ,经过判断当a=
,经过判断当a=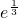 时,b(a)为极大值,即b的最大值;
时,b(a)为极大值,即b的最大值;

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<