
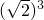 为无理数q:
为无理数q: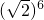 为无理数
为无理数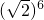 =8为有理数,
=8为有理数,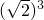 =2
=2 为无理数,正确;q:
为无理数,正确;q: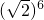 =8为无理数,错,因此“p或q”是真命题;
=8为无理数,错,因此“p或q”是真命题;

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
| A、p:2为质数q:1为质数 | ||||
B、p:(
| ||||
| C、p:奇数集为x|x=4n+1,n∈Zq:偶数集为{x|x=4n,n∈Z} | ||||
| D、p:CIA∪CIB=CI(A∩B)q:CIA∩CIB=CI(A∪B) |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.正数或负数的倒数是正数
B.当a=0且b=0时a2+b2=0
C.方程x2+1=0无实数根
D.李敏在足球队中既是队员,又是教练
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.p:2为质数q:1为质数 | ||||
B.p:(
| ||||
| C.p:奇数集为x|x=4n+1,n∈Zq:偶数集为{x|x=4n,n∈Z} | ||||
| D.p:CIA∪CIB=CI(A∩B)q:CIA∩CIB=CI(A∪B) |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省益阳十六中高一(上)期末数学试卷(解析版) 题型:选择题
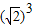 为无理数q:
为无理数q: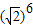 为无理数
为无理数查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com