
| |||||||||||
(1) |
解:因为OE=1,EF= 当α∈[ 所以f(α)=S△AOB= 当α∈[ 所以f(α)=S△AOB= 综上,得f(α)= |
(2) |
解:由(1)得,当α∈[0, f(α)= 当α∈[ 故f(α)的取值范围为[ 分析:本题主要考查三角形的有关知识及三角函数在求函数最值方面的应用.由OE、EF的长知要讨论α的范围.再根据三角形的边角关系列出△AOB的面积,再求函数最值. |


科目:高中数学 来源: 题型:
 如图所示,A、B是在同一水平面上相距am的两处雷达站,A在B的正西方,突然两台雷达同时发现天空O位置处一不明飞行物正以100
如图所示,A、B是在同一水平面上相距am的两处雷达站,A在B的正西方,突然两台雷达同时发现天空O位置处一不明飞行物正以100| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2014届江西省高一下学期第一次月考数学试卷 题型:解答题
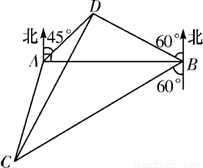
如图所示,A,B是海面上位于东西方向相距5(3+)海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救,其航行速度为30海里/小时,则该救援船到达D点需要多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,A,B是海面上位于东西方向相距5(3+![]() )海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20![]() 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,则该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,则该救援船到达D点需要多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com