
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() (
(![]() )个单位长度后得到函数
)个单位长度后得到函数![]() 的图象,若
的图象,若![]() 在区间
在区间![]() 上单调递增,则实数
上单调递增,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:根据平移关系求出g(x)的解析式,结合函数的单调性建立不等式关系进行求解即可.
详解:将函数f(x)=sin2x的图象向右平移φ(0<![]() <
<![]() )个单位长度后得到函数g(x)的图象,
)个单位长度后得到函数g(x)的图象,
则g(x)=sin2(x﹣![]() )=sin(2x﹣2
)=sin(2x﹣2![]() ),
),
若g(x)在区间[0,![]() ]上单调递增,
]上单调递增,
则2kπ﹣![]() ≤2x﹣2
≤2x﹣2![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,
,k∈Z,
得2kπ﹣![]() +2
+2![]() ≤2x≤2kπ+
≤2x≤2kπ+![]() +2
+2![]() ,k∈Z,
,k∈Z,
即kπ﹣![]() +
+![]() ≤x≤kπ+
≤x≤kπ+![]() +
+![]() ,k∈Z,
,k∈Z,
即函数的单调递增区间为[kπ﹣![]() +
+![]() ,kπ+
,kπ+![]() +
+![]() ],k∈Z,
],k∈Z,
∵若g(x)在区间[0,![]() ]上单调递增,
]上单调递增,
∴满足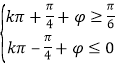 ,即
,即 ,
,
则﹣kπ﹣![]() ≤
≤![]() ≤﹣kπ+
≤﹣kπ+![]() ,k∈Z,
,k∈Z,
当k=0时,﹣![]() ≤
≤![]() ≤
≤![]() ,
,
又因为:0<![]() <
<![]()
所以![]() 的取值范围是(0,
的取值范围是(0,![]() ],
],
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).

(1)当![]() 时,作出
时,作出![]() 的图象,并写出它的单调递增区间;
的图象,并写出它的单调递增区间;
(2)设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)已知函数![]() 在
在![]() 的情况下:其在区间
的情况下:其在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.设
单调递增.设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条街道上有10盏路灯,将路灯依次排列并编号1到10.有关部门要求晚上这10盏路灯中相邻的两盏灯不能全开,且这10盏路灯中至少打开两盏路灯.则符合要求的开法总数______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①对于独立性检验,![]() 的值越大,说明两事件相关程度越大;②以模型
的值越大,说明两事件相关程度越大;②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和
和![]() ;③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程
;③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() ;④通过回归直线
;④通过回归直线![]() 及回归系数
及回归系数![]() ,可以精确反映变量的取值和变化趋势,其中正确的个数是( )
,可以精确反映变量的取值和变化趋势,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,底面ABC为正三角形,
中,底面ABC为正三角形,![]() 底面ABC,
底面ABC,![]() ,点
,点![]() 在线段
在线段![]() 上,平面
上,平面![]() 平面
平面![]() .
.

(1)请指出点![]() 的位置,并给出证明;
的位置,并给出证明;
(2)若![]() ,求
,求![]() 与平面ABE夹角的正弦值.
与平面ABE夹角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com