
【题目】已知数列{an}的前n项和为Sn,满足Sn=2an-1(n∈N*),数列{bn}满足nbn+1-(n+1)bn=n(n+1)(n∈N*),且b1=1.
(1)证明数列{![]() }为等差数列,并求数列{an}和{bn}的通项公式;
}为等差数列,并求数列{an}和{bn}的通项公式;
(2)若cn=(-1)n-1![]() ,求数列{cn}的前n项和T2n;
,求数列{cn}的前n项和T2n;
(3)若dn=an![]() ,数列{dn}的前n项和为Dn,对任意的n∈N*,都有Dn≤nSn-a,求实数a的取值范围.
,数列{dn}的前n项和为Dn,对任意的n∈N*,都有Dn≤nSn-a,求实数a的取值范围.
【答案】(1)证明见解析,an=2n-1,bn=n2 (2)![]() (3)(-∞,0]
(3)(-∞,0]
【解析】
(1)Sn=2an﹣1(n∈N*),n≥2时,an=Sn﹣Sn﹣1=2an﹣1﹣(2an﹣1﹣1),化为:an=2an﹣1.利用等比数列的通项公式可得an.数列{bn}满足nbn+1﹣(n+1)bn=n(n+1)(n∈N*),化为:![]() 1,且b1=1.即可证明数列{
1,且b1=1.即可证明数列{![]() }为等差数列,利用通项公式可得bn.
}为等差数列,利用通项公式可得bn.
(2)cn=(﹣1)n﹣1![]() (﹣1)n﹣1
(﹣1)n﹣1![]() (﹣1)n﹣1
(﹣1)n﹣1![]() ,利用裂项求和方法即可得出.
,利用裂项求和方法即可得出.
(3)dn=an![]() n2n﹣1,利用错位相减法可得数列{dn}的前n项和为Dn,又Sn=2n﹣1.代入对任意的n∈N*,都有Dn≤nSn﹣a,即可得出.
n2n﹣1,利用错位相减法可得数列{dn}的前n项和为Dn,又Sn=2n﹣1.代入对任意的n∈N*,都有Dn≤nSn﹣a,即可得出.
(1)Sn=2an﹣1(n∈N*),n≥2时,an=Sn﹣Sn﹣1=2an﹣1﹣(2an﹣1﹣1),化为:an=2an﹣1.
n=1时,a1=2a1﹣1,解得a1=1.
∴数列{an}是等比数列,公比为2.
∴an=2n﹣1.
数列{bn}满足nbn+1﹣(n+1)bn=n(n+1)(n∈N*),
化为:![]() 1,且b1=1.
1,且b1=1.
∴数列{![]() }为等差数列,公差为1,首项为
}为等差数列,公差为1,首项为![]() 1.
1.
∴![]() 1+n﹣1=n,
1+n﹣1=n,
bn=n2.
(2)cn=(﹣1)n﹣1![]() (﹣1)n﹣1
(﹣1)n﹣1![]() (﹣1)n﹣1
(﹣1)n﹣1![]() ,
,
∴数列{cn}的前n项和T2n![]()
![]()
![]() .
.
(3)dn=an![]() n2n﹣1,
n2n﹣1,
数列{dn}的前n项和为Dn=1+2×2+3×22+……+n2n﹣1,
2Dn=2+2×22+……+(n﹣1)2n﹣1+n2n,
∴﹣Dn=1+2+22+……+2n﹣1﹣n2n![]() n2n,
n2n,
解得Dn=(n﹣1)2n+1.
Sn=2an﹣1=2n﹣1.
对任意的n∈N*,都有Dn≤nSn﹣a,
∴a≤n(2n﹣1)﹣(n﹣1)2n﹣1=2n﹣n﹣1.
令dn=2n﹣n﹣1.则dn+1﹣dn=2n+1﹣(n+1)﹣1﹣(2n﹣n﹣1)=2n﹣1>0.
∴数列{dn}单调递增.
∴a≤(dn)min=d1=0.
∴实数a的取值范围是(﹣∞,0].


科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两校学生自主招生通过情况,从甲校抽取60人,从乙校抽取50人进行分析。

(1)根据题目条件完成上面2×2列联表,并据此判断是否有99%的把握认为自主招生通过情况与学生所在学校有关;
(2)现已知甲校![]() 三人在某大学自主招生中通过的概率分别为
三人在某大学自主招生中通过的概率分别为![]() ,
,![]() ,
,![]() ,用随机变量X表示
,用随机变量X表示![]() 三人在该大学自主招生中通过的人数,求X的分布列及期望
三人在该大学自主招生中通过的人数,求X的分布列及期望![]() .
.
参考公式:![]() .
.
参考数据:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以教材第82页第8题的函数![]() 为基本素材,研究该函数的相关性质,取得部分研究成果如下:
为基本素材,研究该函数的相关性质,取得部分研究成果如下:
①同学甲发现:函数![]() 的定义域为
的定义域为![]() ;
;
②同学乙发现:函数![]() 是偶函数;
是偶函数;
③同学丙发现:对于任意的![]() 都有
都有![]() ;
;
④同学丁发现:对于任意的![]() ,都有
,都有![]() ;
;
⑤同学戊发现:对于函数![]() 定义域中任意的两个不同实数
定义域中任意的两个不同实数![]() ,总满足
,总满足![]() .
.
其中所有正确研究成果的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位幼儿园老师给班上k(k≥3)个小朋友分糖果.她发现糖果盒中原有糖果数为a0,就先从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的![]() 分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
(1)当k=3,a0=12时,分别求a1,a2,a3;
(2)请用an-1表示an;令bn=(n+1)an,求数列{bn}的通项公式;
(3)是否存在正整数k(k≥3)和非负整数a0,使得数列{an}(n≤k)成等差数列,如果存在,请求出所有的k和a0,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月18日,举世瞩目的第18届亚运会在印尼首都雅加达举行,为了丰富亚运会志愿者的业余生活,同时鼓励更多的有志青年加入志愿者行列,大会主办方决定对150名志愿者组织一次有关体育运动的知识竞赛(满分120分)并计划对成绩前15名的志愿者进行奖励,现将所有志愿者的竞赛成绩制成频率分布直方图,如图所示,若第三组与第五组的频数之和是第二组的频数的3倍,试回答以下问题:
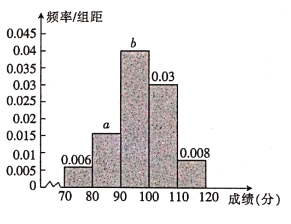
(1)求图中![]() 的值;
的值;
(2)求志愿者知识竞赛的平均成绩;
(3)从受奖励的15人中按成绩利用分层抽样抽取5人,再从抽取的5人中,随机抽取2人在主会场服务,求抽取的这2人中其中一人成绩在![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(江苏省南京师大附中2018届高三高考考前模拟考试数学试题)已知等差数列{an}和等比数列{bn}均不是常数列,若a1=b1=1,且a1,2a2,4a4成等比数列, 4b2,2b3,b4成等差数列.
(1)求{an}和{bn}的通项公式;
(2)设m,n是正整数,若存在正整数i,j,k(i<j<k),使得ambj,amanbi,anbk成等差数列,求m+n的最小值;
(3)令cn=![]() ,记{cn}的前n项和为Tn,{
,记{cn}的前n项和为Tn,{![]() }的前n项和为An.若数列{pn}满足p1=c1,且对n≥2, n∈N*,都有pn=
}的前n项和为An.若数列{pn}满足p1=c1,且对n≥2, n∈N*,都有pn=![]() +Ancn,设{pn}的前n项和为Sn,求证:Sn<4+4lnn.
+Ancn,设{pn}的前n项和为Sn,求证:Sn<4+4lnn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,…以此类推:记格点坐标为
,…以此类推:记格点坐标为![]() 的点(
的点(![]() 均为正整数)处所标的数字为
均为正整数)处所标的数字为![]() ,若
,若![]() ,则
,则![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com