Question

某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)

Answer 1

巨响发生在接报中心的西偏北45⁰距中心处.

解析:

【解题思路】时间差即为距离差，到两定点距离之差为定值的点的轨迹是双曲线型的．

如图，以接报中心为原点O，正东、正北方向为x轴、y轴正向，建立直角坐标系.设A、B、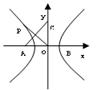

C分别是西、东、北观测点，则A（－1020，0），B（1020，0），C（0，1020）

设P（x,y）为巨响为生点，由A、C同时听到巨响声，得|PA|=|PC|，故P在AC的垂直平分线PO上，PO的方程为y=－x，因B点比A点晚4s听到爆炸声，故|PB|－ |PA|=340×4=1360

由双曲线定义知P点在以A、B为焦点的双曲线上，

依题意得a=680, c=1020，

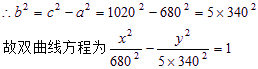
用y=－x代入上式，得，∵|PB|>|PA|,

答：巨响发生在接报中心的西偏北45⁰距中心处.

【名师指引】解应用题的关键是将实际问题转换为“数学模型”