
 现在“汽车”是很“给力”的名词.汽车厂商对某款汽车的维修费进行电脑模拟试验,分别以汽车使用年限n和前n年累计维修费Sn(万元)为横、纵坐标绘制成点,发现点(n,Sn)在函数y=ax2+bx(a≠0)的图象上(如图所示),其中A(5,1.05)、B(10,4.1).
现在“汽车”是很“给力”的名词.汽车厂商对某款汽车的维修费进行电脑模拟试验,分别以汽车使用年限n和前n年累计维修费Sn(万元)为横、纵坐标绘制成点,发现点(n,Sn)在函数y=ax2+bx(a≠0)的图象上(如图所示),其中A(5,1.05)、B(10,4.1). )
)
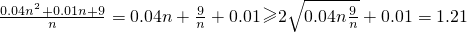 万元
万元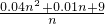 ,利用基本不等式可求
,利用基本不等式可求

科目:高中数学 来源: 题型:
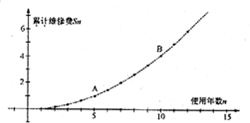 现在“汽车”是很“给力”的名词.汽车厂商对某款汽车的维修费进行电脑模拟试验,分别以汽车使用年限n和前n年累计维修费Sn(万元)为横、纵坐标绘制成点,发现点(n,Sn)在函数y=ax2+bx(a≠0)的图象上(如图所示),其中A(5,1.05)、B(10,4.1).
现在“汽车”是很“给力”的名词.汽车厂商对某款汽车的维修费进行电脑模拟试验,分别以汽车使用年限n和前n年累计维修费Sn(万元)为横、纵坐标绘制成点,发现点(n,Sn)在函数y=ax2+bx(a≠0)的图象上(如图所示),其中A(5,1.05)、B(10,4.1).| 车价+车主承担的维修费 | 使用年数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:湖南省月考题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:月考题 题型:解答题
 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com