
【题目】某科技博览会展出的智能机器人有 A,B,C,D 四种型号,每种型号至少有 4 台.要求每 位购买者只能购买1台某种型号的机器人,且购买其中任意一种型号的机器人是等可能的.现在有 4 个人要购买机器人.
(Ⅰ)在会场展览台上,展出方已放好了 A,B,C,D 四种型号的机器人各一台,现把他们 排成一排表演节目,求 A 型与 B 型相邻且 C 型与 D 型不相邻的概率;
(Ⅱ)设这 4 个人购买的机器人的型号种数为ξ,求ξ 的分布列和数学期望.
【答案】解:(I) A 型与 B 型相邻且 C 型与 D 型不相邻只能是C、AB、D,或C、BA、D,C,D也可以交换. 因此概率P= ![]() =
= ![]() .
.
(II)ξ的可能取值为1,2,3,4.
P(ξ=1)= ![]() =
= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() =
= ![]() ,P(ξ=4)=
,P(ξ=4)= ![]() =
= ![]() ,P(ξ=3)=
,P(ξ=3)= ![]() =.
=. ![]()
∴
ξ | 1 | 2 | 3 | 4 |
P |
|
|
|
|
∴E(ξ)=1× ![]() +2×
+2× ![]() +4×
+4× ![]() +3×
+3× ![]() =
= ![]()
【解析】(I) 四中机器人的总的排序为 ![]() ,A 型与 B 型相邻且 C 型与 D 型不相邻只能是C、AB、D,或C、BA、D,C,D也可以交换.(II)ξ的可能取值为1,2,3,4.P(ξ=1)=
,A 型与 B 型相邻且 C 型与 D 型不相邻只能是C、AB、D,或C、BA、D,C,D也可以交换.(II)ξ的可能取值为1,2,3,4.P(ξ=1)= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() ,P(ξ=4)=
,P(ξ=4)= ![]() ,P(ξ=3)=
,P(ξ=3)= ![]() ,即可得出.
,即可得出.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.
(Ⅰ)求证:BE=DE;
(Ⅱ)若AB=2 ![]() ,AE=3
,AE=3 ![]() ,平面EBD⊥平面ABCD,直线AE与平面ABD所成的角为45°,求二面角B﹣AE﹣D的余弦值.
,平面EBD⊥平面ABCD,直线AE与平面ABD所成的角为45°,求二面角B﹣AE﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣1﹣a(x+lnx),a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线为x轴,求a的值:
(2)在(1)的条件下,求f(x)的单调区间;
(3)若x>0,f(x)≥f(m)恒成立,且f(m)≥0,求证:f(m)≥2(m2﹣m3).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中有7个大小相同的小球,其中有2个红球,3个黄球,2个蓝球,从中任取3个小球.
(I)求红、黄、蓝三种颜色的小球各取1个的概率;
(II)设X表示取到的蓝色小球的个数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 C1: ![]() =1( a>0,b>0),圆 C2:x2+y2﹣2ax+
=1( a>0,b>0),圆 C2:x2+y2﹣2ax+ ![]() a2=0,若双曲线C1 的一条渐近线与圆 C2 有两个不同的交点,则双曲线 C1 的离心率的范围是( )
a2=0,若双曲线C1 的一条渐近线与圆 C2 有两个不同的交点,则双曲线 C1 的离心率的范围是( )
A.(1, ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,P是双曲线在第一象限上的点且满足|PF1|=2|PF2|,直线PF2交双曲线C于另一点N,又点M满足
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,P是双曲线在第一象限上的点且满足|PF1|=2|PF2|,直线PF2交双曲线C于另一点N,又点M满足 ![]() =
= ![]() 且∠MF2N=120°,则双曲线C的离心率为( )
且∠MF2N=120°,则双曲线C的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2+lnx,a∈R. (Ⅰ)若曲线y=f(x)与直线y=3x+b在x=1处相切,求实数a,b的值;
ax2+lnx,a∈R. (Ⅰ)若曲线y=f(x)与直线y=3x+b在x=1处相切,求实数a,b的值;
(Ⅱ)求函数y=f(x)的单调区间;
(Ⅲ)若a=0时,函数h(x)=f(x)+bx有两个不同的零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程ρ=2cosθ,直线l的参数方程是 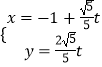 (t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设直线l与y轴的交点是M,N是曲线C上一动点,求|MN|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 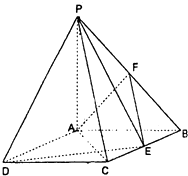
(1)证明:无论点E在BC边的何处,都有PE⊥AF;
(2)当BE等于何值时,PA与平面PDE所成角的大小为45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com