解:
(1)根据题意,得f(x)=|x
2-2x|=
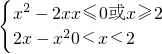
.
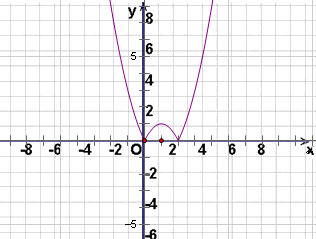
∴当x≤0或x≥2时,图象为抛物线开口向上的部分;当0<x<2时,图象为抛物线开口向下的部分,
可得函数图象如图所示 …(5分)
(2)由(1)得,函数的单调减区间为(-2,0)和(1,2);
单调增区间为(0,1)和(2,6).…(9分)
(3)∵方程f(x)=a在区间[-2,6]有两个不同的实数根,
f(0)=f(2)=0,f(1)=1且f(-2)=f(4)=8
∴a=0或1<a≤8 …(14分)
分析:(1)根据二次函数图象,结合y=|f(x)|的图象的变换规律,得到牛族动物f(x)=|x
2-2x|的函数图象如图所示;
(2)根据(1)作出的函数图象,结合二次函数的单调性,可得函数的单调减区间为(-2,0)和(1,2);单调增区间为(0,1)和(2,6).
(3)由y=|f(x)|的图象,知当a=0时,方程f(x)=a有两个实数根,而f(1)=1、f(-2)=f(4)=8,所以1<a≤8 时方程方程f(x)=a有两个实数根,故当a=0或1<a≤8时,方程f(x)=a在区间[-2,6]有两个不同的实数根.
点评:本题给出含有绝对值的二次函数,求作函数的图象并且求函数的单调区间,着重考查了二次函数的单调性和带绝对值的函数图象等知识点,属于中档题.

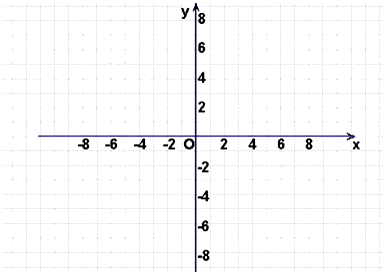 设函数f(x)=|x2-2x|.
设函数f(x)=|x2-2x|.
 .
.

 名校课堂系列答案
名校课堂系列答案