
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:不详 题型:解答题
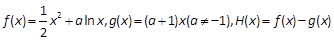 。
。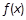 的单调减区间是
的单调减区间是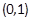 ,求实数a的值;
,求实数a的值;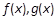 在区间
在区间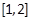 上都为单调函数且它们的单调性相同,求实数a的取值范围;
上都为单调函数且它们的单调性相同,求实数a的取值范围;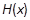 的两个极值点,a<b,
的两个极值点,a<b,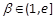 。求证:对任意的
。求证:对任意的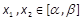 ,不等式
,不等式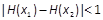 成立.
成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
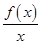 在区间(1,+∞)上一定( )
在区间(1,+∞)上一定( )| A.有最小值 | B.有最大值 | C.是减函数 | D.是增函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
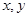 轴上滑动,点M在线段AB上,且
轴上滑动,点M在线段AB上,且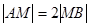 ,
,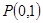 的直线
的直线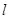 与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求
与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求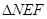 面积的最大值.
面积的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com