
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点相同,A为椭圆C的右顶点,以A为圆心的圆与直线
的焦点相同,A为椭圆C的右顶点,以A为圆心的圆与直线![]() 相交于P,
相交于P, ![]() 两点,且
两点,且![]()
(Ⅰ)求椭圆C的标准方程和圆A的方程;

(Ⅱ)不过原点的直线![]() 与椭圆C交于M、N两点,已知OM,直线
与椭圆C交于M、N两点,已知OM,直线![]() ,ON的斜率
,ON的斜率![]() 成等比数列,记以OM、ON为直径的圆的面积分别为S1、S2,试探究
成等比数列,记以OM、ON为直径的圆的面积分别为S1、S2,试探究![]() 的值是否为定值,若是,求出此值;若不是,说明理由.
的值是否为定值,若是,求出此值;若不是,说明理由.
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是函数
是函数![]() 的图像上任意不同的两点,依据图像可知,线段
的图像上任意不同的两点,依据图像可知,线段![]() 总是位于
总是位于![]() 两点之间函数图像的上方,因此有结论
两点之间函数图像的上方,因此有结论![]() 成立,运用类比的思想方法可知,若点
成立,运用类比的思想方法可知,若点![]() ,
,![]() 是函数
是函数![]() 的图像上任意不同的两点,则类似地有_________成立.
的图像上任意不同的两点,则类似地有_________成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD⊥平面PCD,PD⊥CD,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2AB, ![]() 为棱PC上一点.
为棱PC上一点.
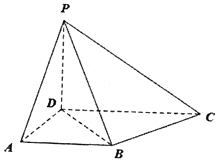
(Ⅰ)若点![]() 是PC的中点,证明:B
是PC的中点,证明:B![]() ∥平面PAD;
∥平面PAD;
(Ⅱ) ![]() 试确定
试确定![]() 的值使得二面角
的值使得二面角![]() -BD-P为60°.
-BD-P为60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() //
//![]() ,
,![]() ,
,![]() 为正三角形. 若
为正三角形. 若![]() ,且
,且![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 是线段
是线段![]() 上一点,记
上一点,记![]() (
(![]() ),是否存在实数
),是否存在实数![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: 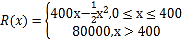 ,其中
,其中![]() 是仪器的月产量.(注:总收益=总成本+利润)
是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图设计一幅矩形宣传画,要求画面面积为4840![]() ,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面高与宽的尺寸,才能使宣传画所用纸张面积最小?
,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面高与宽的尺寸,才能使宣传画所用纸张面积最小?
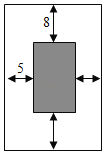
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长,设某地区城乡居民人民币储蓄存款![]() (单位:亿元)的数据如下:
(单位:亿元)的数据如下:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)2018年城乡居民储蓄存款前五名中,有三男和两女.现从这5人中随机选出2人参加某访谈节目,求选中的2人性别不同的概率.
附:回归直线的斜率和截距的最小二乘估计公式分别为:  ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
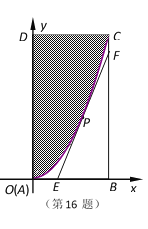
【题目】国务院批准从2009年起,将每年8月8日设置为“全民健身日”,为响应国家号召,各地利用已有土地资源建设健身场所.如图,有一个长方形地块![]() ,边
,边![]() 为
为![]() ,
,![]() 为
为![]() .地块的一角是草坪(图中阴影部分),其边缘线
.地块的一角是草坪(图中阴影部分),其边缘线![]() 是以直线
是以直线![]() 为对称轴,以
为对称轴,以![]() 为顶点的抛物线的一部分.现要铺设一条过边缘线
为顶点的抛物线的一部分.现要铺设一条过边缘线![]() 上一点
上一点![]() 的直线型隔离带
的直线型隔离带![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的△
上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的△![]() 作为健身场所.则△
作为健身场所.则△![]() 的面积为
的面积为![]() 的最大值为____________(单位:
的最大值为____________(单位:![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com