
【题目】已知函数f(x)![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f(![]() )
)![]() ,
,
(1)确定函数的解析式;
(2)用定义法判断函数的单调性;
(3)解不等式;f(t﹣1)+f(t)<0.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】某美术学院2018年在山西招生,报名人数很多.工作人员在某个市区抽取了该区2018年美术招生考试成绩中200名学生的色彩和素描的初试成绩,按成绩分组,得到的频率分布表如下图所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 24 | 0.12 |
第2组 |
| ① | 0.18 |
第3组 |
| 64 | 0.32 |
第4组 |
| 60 | ② |
第5组 |
| 16 | 0.08 |
合计 | 200 | 1.00 | |
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图,并由频率分布直方图估算中位数;
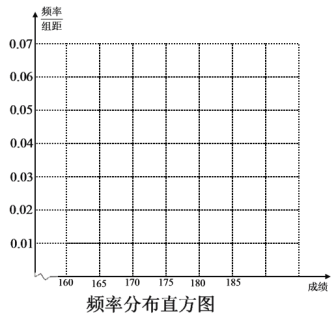
(2)为了能更清楚地了解该市学生的情况,该美院决定在复试以前先进行抽样调研.但受场地和教授人数的客观限制,决定从第3组选出3人,第4组选出2人,第5组选出1人,然后从这6人中再选出2人进行调研,求这2人均来自第三组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲市有![]() 万名高三学生参加了天一大联考,根据学生数学成绩(满分:
万名高三学生参加了天一大联考,根据学生数学成绩(满分:![]() 分)的大数据分析可知,本次数学成绩
分)的大数据分析可知,本次数学成绩![]() 服从正态分布,即
服从正态分布,即![]() ,且
,且![]() ,
,![]() .
.
(1)求![]() 的值.
的值.
(2)现从甲市参加此次联考的高三学生中,随机抽取![]() 名学生进行问卷调查,其中数学成绩高于
名学生进行问卷调查,其中数学成绩高于![]() 分的人数为
分的人数为![]() ,求
,求![]() .
.
(3)与甲市相邻的乙市也有![]() 万名高三学生参加了此次联考,且其数学成绩
万名高三学生参加了此次联考,且其数学成绩![]() 服从正态分布
服从正态分布![]() .某高校规定此次联考数学成绩高于
.某高校规定此次联考数学成绩高于![]() 分的学生可参加自主招生考试,则甲和乙哪个城市能够参加自主招生考试的学生更多?
分的学生可参加自主招生考试,则甲和乙哪个城市能够参加自主招生考试的学生更多?
附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣4x2+5x﹣4.
(1)求曲线f(x)在点(2,f(2))处的切线方程:
(2)若g(x)=f(x)+k,求g(x)的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 为常数,且
为常数,且![]() )满足条件:
)满足条件:![]() ,且方程
,且方程![]() 有两相等实根.
有两相等实根.
(1)求![]() 的解析式;
的解析式;
(2)设命题![]() “函数
“函数![]() 在
在![]() 上有零点”,命题
上有零点”,命题![]() “函数
“函数![]() 在
在![]() 上单调递增”;若命题“
上单调递增”;若命题“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1与圆O:x2+y2=r(r>0)交于点P(﹣1,y0).且关于直线x+y=1对称.
(1)求圆O及圆O1的方程:
(2)在第一象限内.圆O上是否存在点A,过点A作直线l与抛物线y2=4x交于点B,与x轴交于点D,且以点D为圆心的圆过点O,A,B?若存在.求出点A的坐标;若不存在.说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com