
【题目】已知椭圆![]() ,长轴长为4,
,长轴长为4,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,点
的左,右焦点,点![]() 是椭圆
是椭圆![]() 上的任意一点,
上的任意一点,![]() 面积的最大为
面积的最大为![]() ,且取得最大值时
,且取得最大值时![]() 为钝角.
为钝角.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,过点
上任意一点,过点![]() 的切线分别交椭圆
的切线分别交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由条件![]() ,当点
,当点![]() 在短轴的端点
在短轴的端点![]()
![]() 或
或![]() 时,
时,![]() 的面积最大得
的面积最大得![]() ,又当
,又当![]() 的面积取得最大值时
的面积取得最大值时![]() 为钝角得
为钝角得 ![]() ,可解出椭圆方程.
,可解出椭圆方程.
(2)分切线的斜率存在和不存在两种情况计算,由![]() ,即
,即![]() 方程联立代入结合直线
方程联立代入结合直线![]() 与圆
与圆![]() 相切计算可得答案.
相切计算可得答案.
(1)设![]() ,
,![]() 短轴的端点分别为
短轴的端点分别为![]() .
.
由椭圆的长轴为4,则![]() .
.
当点![]() 在短轴的端点
在短轴的端点![]()
![]() 或
或![]() 时,
时,![]() 的面积最大,则
的面积最大,则![]() ……
……![]()
当![]() 的面积取得最大值时
的面积取得最大值时![]() 为钝角.
为钝角.
即![]() ,所以
,所以![]() ,即
,即![]() ……………
……………![]()
又![]() ………
………![]()
由![]()
![]()
![]() 解得:
解得:![]()
所以椭圆方程为:![]() .
.
(2)设圆![]() 上过点
上过点![]() 的切线为直线
的切线为直线![]() .
.
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,则
,则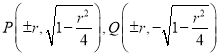
由![]() ,即
,即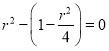 ,解得:
,解得:![]() .
.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]()
由直线![]() 与圆
与圆![]() 相切得:
相切得:![]() 即:
即:![]() .
.
设![]()
由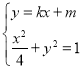 得:
得:![]()
则![]()
由![]() ,即
,即![]()
所以![]() ,即
,即![]()
所以![]()
即![]() ,则
,则![]() .
.
由![]() 得
得![]() .
.
所以![]() .
.
综上所述![]() 的值为
的值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知四棱锥中![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的中点,直线
上的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,点
,点![]() 在
在![]() 上移动.
上移动.
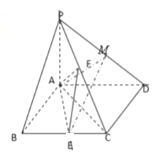
(Ⅰ)证明:无论点![]() 在
在![]() 上如何移动,都有平面
上如何移动,都有平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 恰为
恰为![]() 的中点时,二面角
的中点时,二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行双12有奖促销活动,顾客购买168元的商品后即可抽奖,抽奖方法是:从装有2个红球![]() 和1个白球
和1个白球![]() 的甲箱与装有2个红球
的甲箱与装有2个红球![]() 和1个白球
和1个白球![]() 的乙箱中,各随机摸出1个球,这些球除颜色,标号外都一样.若摸出的2个球颜色相同则中奖,否则不中奖.
的乙箱中,各随机摸出1个球,这些球除颜色,标号外都一样.若摸出的2个球颜色相同则中奖,否则不中奖.
(1)用球的标号列出所有可能的摸出结果;
(2)小明根据经验认为:摸到同色球一般来说更为难得,所以猜测中奖的概率小于不中奖的概率,你认为小明的猜想正确吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 是圆心在极轴上且经过极点的圆,射线
是圆心在极轴上且经过极点的圆,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的参数方程,
的参数方程,![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的两点,求
上的两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)已知![]() 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当![]() 时,有
时,有![]() .若
.若![]() ,且
,且![]() ,求函数
,求函数![]()
![]() 的反函数;
的反函数;
(3)若在![]() 上存在
上存在![]() 个不同的点
个不同的点![]() ,
,![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收入
收入![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用
专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用![]() 等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | 四级 |
|
每月应纳税所得额(含税) | 不超过3000元的部分 | 超过3000元至12000元的部分 | 超过12000元至25000元的部分 | 超过25000元至35000元的部分 |
|
税率 | 3 | 10 | 20 | 25 |
|
(1)现有李某月收入29600元,膝下有一名子女,需要赡养老人,除此之外,无其它专项附加扣除.请问李某月应缴纳的个税金额为多少?
(2)为研究月薪为20000元的群体的纳税情况,现收集了某城市500名的公司白领的相关资料,通过整理资料可知,有一个孩子的有400人,没有孩子的有100人,有一个孩子的人中有300人需要赡养老人,没有孩子的人中有50人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的500人中,任何两人均不在一个家庭).若他们的月收入均为20000元,依据样本估计总体的思想,试估计在新个税政策下这类人群缴纳个税金额![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com