
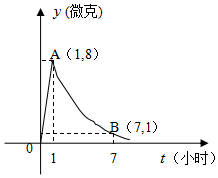
 某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升中的含药量y(微克)与服药的时间t(小时)之间近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.
某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升中的含药量y(微克)与服药的时间t(小时)之间近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.分析 (1)由题设条件中的图象,利用数形结合思想能求出服药后y与t之间的函数关系式;
(2)令$8\sqrt{2}•{(\frac{{\sqrt{2}}}{2})^t}≥2$,解得t≤5,由此能求出第二次服药最迟时间.
解答 解:(1)当0≤t<1时,y=8t;
当t≥1时,$\left\{\begin{array}{l}ka=8\\ k{a^7}=1\end{array}\right.$,所以$\left\{\begin{array}{l}a=\frac{{\sqrt{2}}}{2}\\ k=8\sqrt{2}\end{array}\right.$,所以$y=\left\{\begin{array}{l}8t(0≤t<1)\\ 8\sqrt{2}{(\frac{{\sqrt{2}}}{2})^t}(t≥1)\end{array}\right.$…(5分)
(2)令$8\sqrt{2}•{(\frac{{\sqrt{2}}}{2})^t}≥2$,解得t≤5
所以第一次服药5小时后,即第二次服药最迟应当在当天上午11时服药…(10分)
点评 本题考查函数关系式的求法,考查函数的生产生活中的实际应用,解题时要认真审题,注意等价转化思想的合理运用.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -1或3 | B. | 1或3 | C. | -1 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-2,0) | C. | (-2,0)∪(2,+∞) | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{15\sqrt{3}}}{4}$ | B. | $\frac{15}{4}$ | C. | $10\sqrt{3}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
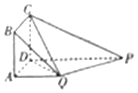 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com