
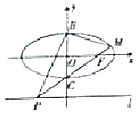
 如图,已知椭圆$\frac{x^2}{a^2}+{y^2}=1(a>1)$的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M,记直线BM,BP的斜率分别为k1,k2.
如图,已知椭圆$\frac{x^2}{a^2}+{y^2}=1(a>1)$的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M,记直线BM,BP的斜率分别为k1,k2.分析 (1)先求出椭圆的方程及焦点坐标,进而可得直线PM的方程,联立直线方程,可得M点坐标,进而可得$\overrightarrow{PB}•\overrightarrow{PM}$的值;
(2)设P(m,-2),由基本不等式可得|k1|+|k2|的最小值时,$m=±2\sqrt{3}$,进而可得直线PM的方程.
解答 解:(1)由椭圆$\frac{x^2}{a^2}+{y^2}=1(a>1)$的长轴长是短轴长的2倍得a=2.…(1分)
由题意B(0,1),C(0,-1),焦点$F(\sqrt{3},0)$,
当直线PM过点F时,则直线PM的方程为$\frac{x}{{\sqrt{3}}}+\frac{y}{-1}=1$,即$y=\frac{{\sqrt{3}}}{3}x-1$,
令y=-2得$x=-\sqrt{3}$,则$P(-\sqrt{3},-2)$.…(3分)
联立$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ y=\frac{{\sqrt{3}}}{3}x-1\end{array}\right.$,
解得$\left\{\begin{array}{l}x=\frac{{8\sqrt{3}}}{7}\\ y=\frac{1}{7}\end{array}\right.$或$\left\{\begin{array}{l}x=0\\ y=-1\end{array}\right.$(舍),即$M(\frac{{8\sqrt{3}}}{7},\frac{1}{7})$.…(4分)
因为$\overrightarrow{PB}=(\sqrt{3},3)$,$\overrightarrow{PM}=(\frac{{15\sqrt{3}}}{7},\frac{15}{7})$,…(5分)
所以$\overrightarrow{PB}•\overrightarrow{PM}=\frac{45}{7}+\frac{45}{7}=\frac{90}{7}$.…(6分)
(2)设P(m,-2),且m≠0,则直线PM的斜率为$k=\frac{-1-(-2)}{0-m}=-\frac{1}{m}$,
则直线PM的方程为$y=-\frac{1}{m}x-1$,…(7分)
联立$\left\{\begin{array}{l}y=-\frac{1}{m}x-1\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$化简得$(1+\frac{4}{m^2}){x^2}+\frac{8}{m}x=0$,解得$M(-\frac{8m}{{{m^2}+4}},\frac{{4-{m^2}}}{{{m^2}+4}})$,…(8分)
所以${k_1}=\frac{{\frac{{4-{m^2}}}{{{m^2}+4}}-1}}{{-\frac{8m}{{{m^2}+4}}}}=\frac{{-2{m^2}}}{-8m}=\frac{1}{4}m$,${k_2}=\frac{1-(-2)}{0-m}=-\frac{3}{m}$,…(10分)
则$|{k_1}|+|{k_2}|=|-\frac{3}{m}|+|\frac{1}{4}m|≥2\sqrt{\frac{3}{4}}=\sqrt{3}$,当且仅当$|-\frac{3}{m}|=|\frac{1}{4}m|$,即$m=±2\sqrt{3}$时取等号.
所以|k1|+|k2|的最小值为$\sqrt{3}$.
此时直线PM的方程为$y=±\frac{{\sqrt{3}}}{6}x-1$.…(12分)
点评 本题考查的知识点是椭圆的标准方程,椭圆的性质,直线与椭圆的位置关系,向量的数量积,基本不等式,难度中档.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{11}{27}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
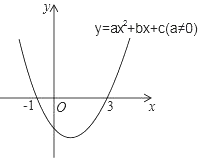 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0;②当-1≤x≤3时,y<0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0;②当-1≤x≤3时,y<0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0其中正确的是( )| A. | ①②④ | B. | ①④ | C. | ①②③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com