
【题目】我国古代数学名著《九章算术》中记载的“刍甍”(chu meng)是指底面为矩形,顶部只有一条棱的五面体.如图,五面体![]() 是一个刍甍,其中
是一个刍甍,其中![]() 是正三角形,
是正三角形,![]() ,则以下两个结论:①
,则以下两个结论:①![]() ;②
;②![]() ,( )
,( )
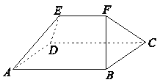
A.①和②都不成立B.①成立,但②不成立
C.①不成立,但②成立D.①和②都成立
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)在第(2)问的条件下,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是演绎推理的个数是( )
①两条直线平行,同旁内角互补。如果∠A与∠B是两条平行直线的同旁内角,那么∠A+∠B=180°;
②猜想数列1,3,5,7,9,11,…的通项公式为![]() ;
;
③由正三角形的性质得出正四面体的性质;
④半径为![]() 的圆的面积
的圆的面积![]() ,则单位圆的面积
,则单位圆的面积![]() .
.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年被称为”新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进.辽宁地区也将于2020年开启新高考模式,今年秋季入学的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为自已将来高考“语数外+3”新高考方案中的“3”.某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模找拟选科数据”调查,每个学生只能从表格中的20种课程组合选择一种学习.模拟选课数据统计如下表 :
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物证历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | … | 40人 | … | … |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | … | … | … | … | … | … | 200人 |
为了解学生成绩与学生模拟选课情况之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析.
(1)从选择学习物理且学习化学的学生中随机抽取3人,求这3人中至少有2天要学习生物的概率;
(2)从选择学习物理且学习化学的学生中随机抽取3人,记这3人中要学习生物的人数为![]() ,要学习政治的人数为
,要学习政治的人数为![]() ,设随机变量
,设随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
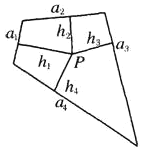
【题目】如图所示,面积为![]() 的平面凸四边形的第
的平面凸四边形的第![]() 条边的边长记为
条边的边长记为![]() ,此四边形内任一点
,此四边形内任一点![]() 到第
到第![]() 条边的距离记为
条边的距离记为![]() ,若
,若![]() ,则
,则![]() .类比以上性质,体积为
.类比以上性质,体积为![]() 的三棱锥的第
的三棱锥的第![]() 个面的面积记为
个面的面积记为![]() ,此三棱锥内任一点
,此三棱锥内任一点![]() 到第
到第![]() 个面的距离记为
个面的距离记为![]() ,若
,若![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是抛物线
是抛物线![]() 上一点,且
上一点,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)过点![]() 作两条互相垂直的直线,与抛物线
作两条互相垂直的直线,与抛物线![]() 的另一交点分别是
的另一交点分别是![]() ,
,![]() .
.
①若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的方程;
的方程;
②若![]() 的面积为12,求
的面积为12,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2-5x+b>0的解是-3<x<2,设A={x|bx2-5x+a>0},B={x|![]() }.
}.
(1)求a,b的值;
(2)求A∩B和A∪(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(单位:辆)与创造的价值y(单位:元)之间有如下的关系:![]() .若这家工厂希望在一个星期内利用这条流水线创收60000元以上,则在一个星期内大约应该生产多少辆摩托车?
.若这家工厂希望在一个星期内利用这条流水线创收60000元以上,则在一个星期内大约应该生产多少辆摩托车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从5本不同的科普书和4本不同的数学书中选出4本,送给4位同学,每人1本,问:
(1)如果科普书和数学书各选2本,共有多少种不同的送法?(各问用数字作答)
(2)如果科普书甲和数学书乙必须送出,共有多少种不同的送法?
(3)如果选出的4本书中至少有3本科普书,共有多少种不同的送法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com