
【题目】已知抛物线C:y2=2px(p>0)的准线方程为x=﹣1.
(1)求抛物线C的方程;
(2)过抛物线C的焦点作直线l,交抛物线C于A,B两点,若线段AB中点的横坐标为6,求|AB|.
【答案】(1)y2=4x;(2)14
【解析】
(1)运用抛物线的准线方程,得到p=2,进而得到抛物线的方程;
(2)设直线l为:x=my+1,与抛物线联立,得到韦达定理,结合中点坐标,即得解m,再利用|AB|=x+x'+p,即得解弦长.
(1)由抛物线的准线得:![]() 1,∴p=2,所以抛物线的方程为:y2=4x;
1,∴p=2,所以抛物线的方程为:y2=4x;
(2)由(1)得焦点F(1,0),又由题意得,显然直线的斜率不为零,
设直线l为:x=my+1,A(x,y),B(x',y'),
联立直线l与抛物线的方程得:
y2﹣4my﹣4=0,
y+y'=4m,x+x'=m(y+y')+2=4m2+2,
由题意得:4m2+2=26=12,
∴|AB|=x+x'+p=12+2=14,
所以弦长|AB|为14.


科目:高中数学 来源: 题型:
【题目】某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食堂用餐的满意度进行评分.根据学生对食堂用餐满意度的评分,得到如图所示的率分布直方图,
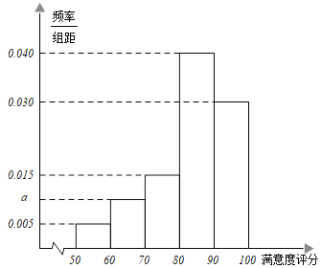
(1)求频率分布直方图中![]() 的值
的值
(2)规定:学生对食堂用餐满意度的评分不低于80分为“满意”,试估计该校在食堂用餐的3000名学生中“满意”的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】贵阳河滨公园是市民休闲游玩的重要场所,某校社团针对“公园环境评价”随机对![]() 位市民进行问卷调查打分(满分100分)得茎叶图如下:
位市民进行问卷调查打分(满分100分)得茎叶图如下:

(1)写出女性打分的中位数和众数;
(2)从打分在![]() 分以下(不含
分以下(不含![]() 分)的市民中随机请
分)的市民中随机请![]() 人进一步提建议,求这
人进一步提建议,求这![]() 人都是男性市民的概率.
人都是男性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
(1)若![]() :
:![]() ;
;![]() :
:![]() ,则
,则![]() 为真,
为真,![]() 为假,
为假,![]() 为真
为真
(2)“![]() ”是“曲线
”是“曲线![]() 表示椭圆”的充要条件
表示椭圆”的充要条件
(3)命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
(4)如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
则正确命题有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() :
:![]() ,以极点
,以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,过点
轴的正半轴建立平面直角坐标系,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为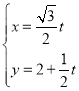 (
(![]() 为参数),点
为参数),点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(Ⅰ)求点![]() 的极坐标;
的极坐标;
(Ⅱ)若点![]() 是曲线
是曲线![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com