
����Ŀ��ij��Ʒ����������ָ��ֱ�Ϊx��y��z�����ۺ�ָ��S=x+y+z���۸ò�Ʒ�ĵȼ�����S��4����ò�ƷΪһ��Ʒ���ִ�һ���ò�Ʒ�У������ȡ10����Ʒ��Ϊ������������ָ���б����£�
��Ʒ��� | A1 | A2 | A3 | A4 | A5 |
����ָ�� | ��1��1��2�� | ��2��1��1�� | ��2��2��2�� | ��1��1��1�� | ��1��2��1�� |
��Ʒ��� | A6 | A7 | A8 | A9 | A10 |
����ָ�� | ��1��2��2�� | ��2��1��1�� | ��2��2��1�� | ��1��1��1�� | ��2��1��2�� |
��1�������ϱ��ṩ���������ݹ��Ƹ�����Ʒ��һ��Ʒ�ʣ�
��2���ڸ���Ʒ��һ��Ʒ�У������ȡ2����Ʒ�� ���ò�Ʒ����г����п��ܵĽ����
�����¼�BΪ����ȡ����2����Ʒ�У�ÿ����Ʒ���ۺ�ָ��S������4�������¼�B�����ĸ��ʣ�
���𰸡�
��1���⣺����10����Ʒ���ۺ�ָ��S�����±�
��Ʒ��� | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
S | 4 | 4 | 6 | 3 | 4 | 5 | 4 | 5 | 3 | 5 |
����S��4����A1��A2��A4��A5��A7��A9����6����
�ʸ�������һ��Ʒ��P=0.6��
�Ӷ��ɹ��Ƹ�����Ʒ��һ��Ʒ��ԼΪ0.6��
��2���⣺���ڸ�������һ��Ʒ�У������ȡ2����Ʒ�����п��ܽ��Ϊ��
��A1��A2������A1��A4������A1��A5������A1��A7������A1��A9����
��A2��A4������A2��A5������A2��A7������A2��A9������A4��A5����
��A4��A7������A4��A9������A5��A7������A5��A9������A7��A9������15�֣�
���ڸ�������һ��Ʒ�У��ۺ�ָ��S����4�IJ�Ʒ��ŷֱ�ΪA1��A2��A5��A7��
���¼�B���������п��ܽ��Ϊ��
��A1��A2������A1��A5������A1��A7������A2��A5������A2��A7������A5��A7������6�֣�
����P��B��= ![]() =
= ![]() ��
��
����������1�����ۺ�ָ��S=x+y+z�����10����Ʒ���ۺ�ָ�겢�б���ʾ����������һ��Ʒ�ʿ���2����ֱ�����оٷ��г��ڸ���Ʒ��һ��Ʒ�У������ȡ2����Ʒ�����еȿ��ܽ�������г���ȡ����2����Ʒ�У�ÿ����Ʒ���ۺ�ָ��S������4�����������Ȼ�����ùŵ�����ʼ��㹫ʽ��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�������������������������⣺�������ѣ�ˮ��ֲ��������һ�գ������ߣ�ݸ��ֲ�������׳�ˮ�С�ϯ�Ӳݣ���һ�գ���һ�ߣ��������룬ݸ�����Ա����ʼ����ն����ȣ�����˼�ǣ�����������1�գ���Ϊ3�ߣ�ݸ����1�գ���Ϊ1�ߣ��ѵ��������ռ��룬ݸ��������������1�������ѡ�ݸ������ȣ��������ʱ��ԼΪ�� �����������һλС�����ο����ݣ�![]() ��
��![]() ���� ��
���� ��
A. 1.3�� B. 1.5�� C. 2.6�� D. 2.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ӷ������˶�Ա�������ܽ���ͳ���о�����������˶�Ա��Ͷ������ʱ���˶�Ա���������ĵ�ˮƽ��������ָ�꣬��ij�˶�Ա���������ɳ��ε�ͳ�ƣ�����ͳ�ƽ����������Ƶ�ʷֲ�ֱ��ͼ��

(I)����Ƶ�ʷֲ�ֱ��ͼ������˶�ԱͶ������ʱ�������������ĵ�ˮƽ�������λ����
(II)��ij�������У�������ǰ4��Ͷ������ʱ���������ĵ�ˮƽ�������������ҹ涨���˶�ԱͶ������ʱ�������������ĵ�ˮƽ���벻����4�ļ�1�֣�����۵�1��.���������X��ʾ��4��Ͷ������ܷ֣���Ƶ����Ϊ���ʣ���X�ķֲ��к;�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��ax+b���ڵ�M��1��f��1�����������߷���Ϊ9x+3y��10=0����
��ax+b���ڵ�M��1��f��1�����������߷���Ϊ9x+3y��10=0����
��1��ʵ��a��b��ֵ��
��2������f��x���ĵ��������Լ�������[0��3]�ϵ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��������������ڼ俪չ��������У��ϵ�ж���������Ϊ�˽ⱾУѧ�������Ķ������ѧУ�����ȡ��100��ѧ����������Ķ�ʱ����е��顣�����Ǹ��ݵ��������Ƶ�ѧ���վ������Ķ�ʱ��(��λ������)��Ƶ�ʷֲ�ֱ��ͼ���ҽ��վ������Ķ�ʱ�䲻����60���ӵ�ѧ����Ϊ����������������60���ӵ�ѧ����Ϊ���Ƕ���������
�Ƕ����� | ������ | �ϼ� | |
�� | 15 | ||
Ů | 45 |

��1��������֪�����������2��2�����������ݴ��ж��Ƿ���99%�İ�����Ϊ�������ԡ����Ա��йأ�
��2�����÷ֲ��������100��ѧ�����������ԡ��г�ȡ8�����м�ѵ������ѡ��2���μ������ж���֪ʶ��������������һ�������μӱ����ĸ��ʡ�
���� 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����߹��㣨2,1���ҹ���![]() ��Գ�.
��Գ�.
��1����������![]() �ķ��̣�
�ķ��̣�
��2����֪Բ������![]() ��Բ��
��Բ��![]() ��������
��������![]() ���˶�����Բ
���˶�����Բ![]() ��
��![]() �ύ��
�ύ��![]() ���㣬��
���㣬��![]() ����
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �ĵױ߳�Ϊ2��
�ĵױ߳�Ϊ2�� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е�.
���е�.
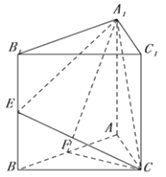
��1����֪![]() Ϊ�߶�
Ϊ�߶�![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ����֤��
����֤�� ![]() ��
��![]() ��
��
��2���������![]() ������ֵΪ
������ֵΪ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=�� ![]() +a��x��a��R
+a��x��a��R
��1�������Ķ�����
��2���Ƿ����ʵ��a��ʹ��f��x��Ϊż������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4-4������ϵ���������]
��ֱ֪��l�IJ�������Ϊ ��tΪ������������C�IJ�������Ϊ
��tΪ������������C�IJ�������Ϊ ����Ϊ��������������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ����P�ļ�����Ϊ
����Ϊ��������������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ����P�ļ�����Ϊ![]() ��
��
������ֱ��l�Լ�����C�ļ����귽�̣�
������ֱ��l������C����A��B���㣬����PAB�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com