
已知在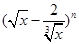 的展开式中,第5项的系数与第3项的系数之比是
的展开式中,第5项的系数与第3项的系数之比是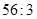 .
.
(1)求展开式中的所有有理项;
(2)求展开式中系数绝对值最大的项;
(3)求 的值.
的值.
(1)有理项为 和
和 ;(2)系数绝对值最大的项为
;(2)系数绝对值最大的项为 ;(3)
;(3) .
.
解析试题分析:(1)先利用二项展开式的通项公式得到第5项的系数与第3项的系数,依题意得到 ,求解可得
,求解可得 ,进而化简该二项展开式的通项公式得到
,进而化简该二项展开式的通项公式得到 ,由
,由 为整数可得出
为整数可得出 的值,进而得到所有的有理项;(2)先求出二项展开式中的系列,并设第
的值,进而得到所有的有理项;(2)先求出二项展开式中的系列,并设第 项系数绝对值最大,列出不等式组
项系数绝对值最大,列出不等式组 ,从中求解即可得出
,从中求解即可得出 的值,进而可写出展开式中系数绝对值最大的项;(3)先根据二项开展式的特征将
的值,进而可写出展开式中系数绝对值最大的项;(3)先根据二项开展式的特征将 变形为
变形为 ,逆用二项式定理即可得结果.
,逆用二项式定理即可得结果.
(1)由 ,解得
,解得 2分
2分
因为通项: 3分
3分
当 为整数,
为整数, 可取0,6 4分
可取0,6 4分
于是有理项为 和
和 6分
6分
(2)设第 项系数绝对值最大,则
项系数绝对值最大,则 (8分)
(8分)
注:等号不写扣(1分)
解得 ,于是
,于是 只能为7 10分
只能为7 10分
所以系数绝对值最大的项为 11分
11分
(3)

 13分
13分 16分
16分
考点:二项式定理及其应用.


科目:高中数学 来源: 题型:解答题
从6名短跑运动员中选出4人参加4×100 m接力赛.试求满足下列条件的参赛方案各有多少种?
(1)甲不能跑第一棒和第四棒;
(2)甲不能跑第一棒,乙不能跑第四棒
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
7名师生站成一排照相留念,其中老师1人,男生4人,女生2人,在下列情况下,各有不同站法多少种?(用数字作答)
(1)两名女生必须相邻而站;
(2)4名男生互不相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
从装有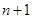 个球(其中
个球(其中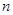 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出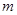 个球
个球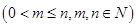 ,共有
,共有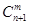 种取法,这
种取法,这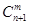 种取法可分成两类:一类是取出的
种取法可分成两类:一类是取出的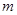 个球中,没有黑球, 有
个球中,没有黑球, 有 种取法,另一类是取出的
种取法,另一类是取出的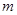 个球中有一个是黑球,有
个球中有一个是黑球,有 种取法,由此可得等式:
种取法,由此可得等式: +
+ =
=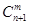 .则根据上述思想方法,当1£k<m<n,k, m, nÎN时,化简
.则根据上述思想方法,当1£k<m<n,k, m, nÎN时,化简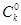 ·
·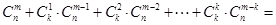 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com