
【题目】选修4-5:不等式选讲
设函数f(x)=x2-x-15,且|x-a|<1,
(1)解不等式![]() ;
;
(2)求证:|f(x)-f(a)|<2(|a|+1).
【答案】(1)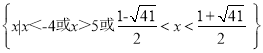 (2)见解析
(2)见解析
【解析】试题分析:(1)先根据绝对值定义将不等式转化为两个一元二次不等式,分别求解,最后求它们的并集(2)作差f(x)-f(a)因式分解得(x-a)(x+a-1),根据条件|x-a|<1以及绝对值三角不等式放缩可得结论
试题解析:(1) 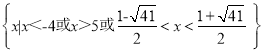
(2)∵|x-a|<1,
∴|f(x)-f(a)|=|(x2-x-15)-(a2-a-15)|
=|(x-a)(x+a-1)|
=|x-a|·|x+a-1|<1·|x+a-1|
=|x-a+2a-1|≤|x-a|+|2a-1|<1+|2a-1|≤1+|2a|+1
=2(|a|+1),
即|f(x)-f(a)|<2(|a|+1).


科目:高中数学 来源: 题型:
【题目】经观测,某公路段在某时段内的车流量y(千辆/小时)与汽车的平均速度v(千/小时)之间有函数关系: ![]()
(1)在该时段内,当汽车的平均速度v为多少时车流量y最大?最大车流量为多少?(精确到0.01千辆);
(2)为保证在该时段内车流量至少为10千辆/小时,则汽车的平均速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①△ABC中角A,B,C的对边分别是a,b,c,若a>b,则cosA<cosB,cos2A<cos2B;
②a,b∈R,若a>b,则a3>b3;
③若a<b,则 ![]() <
< ![]() ;
;
④设等差数列{an}的前n项和为Sn , 若S2016﹣S1=1,则S2017>1.
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.
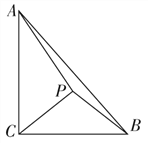
(1)若P是等腰直角三角形PBC的直角顶点,求PA的长;
(2)若∠BPC=![]() ,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}是单调递增的数列,a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=anlog2an , 数列{bn}的前n项和为Sn , 求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,分别是椭圆
,分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若点![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com