
【题目】如图:在四棱锥E﹣ABCD中,CB=CD=CE=1,AB=AD=AE= ![]() ,EC⊥BD,底面四边形是个圆内接四边形,且AC是圆的直径.
,EC⊥BD,底面四边形是个圆内接四边形,且AC是圆的直径.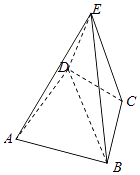
(1)求证:平面BED⊥平面ABCD;
(2)点P是平面ABE内一点,满足DP∥平面BEC,求直线DP与平面ABE所成角的正弦值的最大值.
【答案】
(1)解:证明:连接AC,BD,交于点O,连接EO,
∵AD=AB,CD=CB∴AC⊥BD,
又∵EC⊥DB,EC∩AC=C,故DB⊥面AEC,从而 BD⊥OE,
又AC是直径∴∠ADC=∠ABC=90°,
由AD= ![]() ,CD=1可解得,AO=
,CD=1可解得,AO= ![]() ,则
,则 ![]() ,故EO⊥AC;
,故EO⊥AC;
故EO⊥平面ABCD,平面BED⊥平面ABCD.…
(2)取AE的中点M,AB的中点N,连接MN,ND,
则MN∥BE,且MN平面EBC,∴MN∥平面EBC;
而DN⊥AB,BC⊥AB,∴DN∥BC,且DN平面EBC,∴DN∥平面EBC.
综上所述,平面DMN∥平面EBC,∴点P在线段MN上.
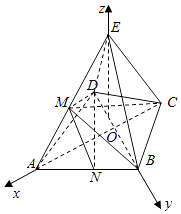
如图建立空间直角坐标系,则A( ![]() ,0,0),B(0,
,0,0),B(0, ![]() ,0),E(0,0,
,0),E(0,0, ![]() ),
),
![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(﹣
=(﹣ ![]() ,0,
,0, ![]() ),
),
设平面ABE法向量为 ![]() =(x,y,z),则
=(x,y,z),则
![]() 取
取 ![]() =(1,
=(1, ![]() ,
, ![]() ),
),
设 ![]() =λ
=λ ![]() ,可得
,可得 ![]() =
= ![]() +
+ ![]() =(
=( ![]() ,
, ![]() , img src="http://thumb.zyjl.cn/questionBank/Upload/2018/02/23/23/7c5b8fc1/SYS201802232334452629765028_DA/SYS201802232334452629765028_DA.016.png" width="51" height="34" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ),
, img src="http://thumb.zyjl.cn/questionBank/Upload/2018/02/23/23/7c5b8fc1/SYS201802232334452629765028_DA/SYS201802232334452629765028_DA.016.png" width="51" height="34" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ),
设直线DP与平面ABE所成角为θ,则sinθ= ![]() .
.
∵0≤λ≤1∴当λ=0时,sinθ的最大值为 ![]() .
.
【解析】(1)由题意可推导出AC⊥BD从而 BD⊥OE,由此能证明直线EO⊥平面ABCD即可得证。(2)根据题意作出辅助线可得出点P在线段MN上建立空间直角坐标系,求出各个点的坐标进而也可求出各个向量的坐标再找出平面ABE的法向量,利用向量法求出即可。
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2 ![]() ,求此时直线l的方程.
,求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”: 2 ![]() =
= ![]() ,3
,3 ![]() =
= ![]() ,4
,4 ![]() =
= ![]() ,5
,5 ![]() =
= ![]()
则按照以上规律,若8 ![]() =
= ![]() 具有“穿墙术”,则n=( )
具有“穿墙术”,则n=( )
A.7
B.35
C.48
D.63
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4 ![]() ,AD=2
,AD=2 ![]() ,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.
,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.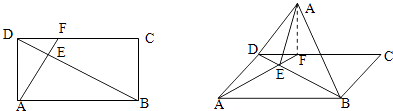
(1)当θ=90°时,求A′C的长;
(2)当cosθ= ![]() 时,求BC与平面A′BD所成角的正弦值.
时,求BC与平面A′BD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)﹣x2+(2﹣a)x﹣a(a∈R)若存在唯一的正整数x0 , 使得f(x0)>0,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ]
]
D.(ln3,ln2+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2x+2 ![]() sinxcosx+a,且当x∈[0,
sinxcosx+a,且当x∈[0, ![]() ]时,f(x)的最小值为2.
]时,f(x)的最小值为2.
(Ⅰ)求a 的值;
(Ⅱ)先将函数y=f (x) 的图象上点的纵坐标不变,横坐标缩小为原来的 ![]() ,再将所得的图象向右平移
,再将所得的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求方程g(x)=4在区间[0,
个单位,得到函数y=g(x)的图象,求方程g(x)=4在区间[0, ![]() ]上所有根之和.
]上所有根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的右准线的方程为x=
(a>b>0)的右准线的方程为x= ![]() ,左、右两个焦点分别为F1(
,左、右两个焦点分别为F1( ![]() ),F2(
),F2( ![]() ).
).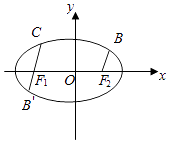
(1)求椭圆E的方程;
(2)过F1 , F2两点分别作两条平行直线F1C和F2B交椭圆E于C,B两点(C,B均在x轴上方),且F1C+F2B等于椭圆E的短轴的长,求直线F1C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com