
【题目】给出的以下四个问题中,不需要用条件语句来描述其算法是( )
A.输入一个实数x,求它的绝对值
B.求面积为6的正方形的周长
C.求三个数a、b、c中的最大数
D.求函数f(x)= ![]() 的值
的值
【答案】B
【解析】解:对于A,输入一个实数x,求它的绝对值,自变量取不同值时,求对应的函数值时,需要代入相应的解析式,需要用条件语句描述. 对于B,求面积为6的正三角形的周长用顺序结构即可,故不需要用条件语句描述;
对于C,求三个数a、b、c中的最大数,由于要作出判断,找出最大数,故本问题的解决要用到条件语句描述;
对于D,因为函数f(x)= ![]() 是一个分段函数,即自变量取不同值时,求对应的函数值时,需要代入相应的解析式,需要用条件语句描述.
是一个分段函数,即自变量取不同值时,求对应的函数值时,需要代入相应的解析式,需要用条件语句描述.
故选:B.
【考点精析】解答此题的关键在于理解算法的条件语句的相关知识,掌握“条件”表示判断的条件;“语句”表示满足条件时执行的操作内容,条件不满足时,结束程序;算机在执行时首先对IF后的条件进行判断,如果条件符合就执行THEN后边的语句,若条件不符合则直接结束该条件语句,转而执行其它语句.


科目:高中数学 来源: 题型:
【题目】在锐角ABC中,角A、B、C所对的边分别为a,b,c,b=4,c=6,且asinB=2![]() .
.
(1)求角A的大小;
(2)若D为BC的中点,求线段AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和a件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出a件正品时检测结束,已知前两次检测都没有检测出次品的概率为![]() .
.
(1) 求实数a的值;
(2) 若每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家秦九韶所著《数学九章》中有“米谷粒分”问题:粮仓开仓收粮,粮农送来米1512石,验得米内夹谷,抽样取米一把,数得216粒内夹谷27粒,则这批米内夹谷约( )
A.164石
B.178石
C.189石
D.196石
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处。
海里处。
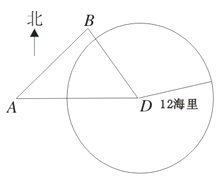
(Ⅰ)求此时该外国船只与![]() 岛的距离;
岛的距离;
(Ⅱ)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行。为了将该船拦截在离
海里的速度沿正南方向航行。为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.
海里内的海域,试确定海监船的航向,并求其速度的最小值.
(参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面区域D由以A(2,4)、B(5,2)、C(3,1)为顶点的三角形内部和边界组成,若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,则m= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com