
(1)(理(1)文(2))若c=5,求sin∠A的值;
(文)若![]() =0,求c的值;
=0,求c的值;
(2)(理)若∠A是钝角,求c的取值范围.
解:(1)(理(1)文(2))解法一:∵A(3,4)、B(0,0),
∴|AB|=5,sin∠B=![]() .
.
当c=5时,|BC|=5,|AC|=![]()
根据正弦定理,得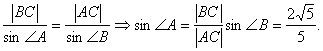
解法二:∵A(3,4)、B(0,0),
∴|AB|=5.
当c=5时,|BC|=5,|AC|=![]()
根据余弦定理,得
cos∠A=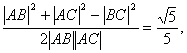
sin∠A=![]() .
.
(文)解法一:∵A(3,4)、B(0,0)、C(c,0),
∴![]() =(-3,-4),
=(-3,-4),![]() =(c-3,-4).
=(c-3,-4).
由![]() ·
·![]() =0
=0![]() (-3)(c-3)+(-4)(-4)=0,
(-3)(c-3)+(-4)(-4)=0,
解得c=![]() .
.
解法二:∵A(3,4)、B(0,0)、C(c,0),
∴|AB|2=32+42=25,|AC|2=(c-3)2+42,|BC|2=c2.
∵![]() ·
·![]() =0,∴AB⊥AC,△ABC是直角三角形.
=0,∴AB⊥AC,△ABC是直角三角形.
根据勾股定理,得|AB|2+|AC|2=|BC|2,
即c2=25+[(c-3)2+42].
解得c=![]() .
.
(2)(理)已知△ABC顶点坐标为A(3,4)、B(0,0)、C(c,0),
∴|AC|2=(c-3)2+42,|BC|2=c2.
根据余弦定理,得cos∠A=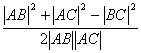 ,
,
若∠A是钝角,则cos∠A<0![]() |AB|2+|AC|2-|BC|2<0,
|AB|2+|AC|2-|BC|2<0,
即52+[(c-3)2+42]-c2=50-6c<0.
解得c>![]() .
.


科目:高中数学 来源: 题型:
 如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,侧面AB1与侧面AC1所成的二面角为60°,M为AA1上的点,∠A1MC1=30°,∠CMC1=90°,AB=a.
如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,侧面AB1与侧面AC1所成的二面角为60°,M为AA1上的点,∠A1MC1=30°,∠CMC1=90°,AB=a.查看答案和解析>>
科目:高中数学 来源:2015届安徽合肥一中高二上学期第一次月考理科数学试卷(解析版) 题型:选择题
已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12.则球O的半径为( )
A. B.2
B.2 C.
C. D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com