已知△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的角平分线所在的直线方程为y=0,点C的坐标为(1,2).
(Ⅰ)求点A和点B的坐标;
(Ⅱ)又过点C作直线l与x轴、y轴的正半轴分别交于点M,N,求△MON的面积最小值及此时直线l的方程.
【答案】
分析:(I)列方程组
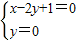
求出A点坐标,根据两直线垂直的条件求出BC、AB所在的直线方程,然后解方程组
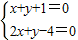
得B的坐标;
(II)若直线分别与x轴、y轴的负半轴交于A,B两点,说明直线的斜率小于0,设出斜率根据直线过的C点,写出直线方程,求出△AOB面积的表达式,利用基本不等式求出面积的最小值,即可得到面积最小值的直线的方程.
解答:解:(Ⅰ)因为点A在BC边上的高x-2y+1=0上,又在∠A的角平分线y=0上,所以解方程组
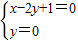
得A(-1,0).
∵BC边上的高所在的直线方程为x-2y+1=0,
∴k
BC=-2,
∵点C的坐标为(1,2),所以直线BC的方程为2x+y-4=0,
∵k
AC=-1,∴k
AB=-k
AC=1,所以直线AB的方程为x+y+1=0,
解方程组
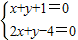
得B(5,-6),
故点A和点B的坐标分别为(-1,0),(5,-6).
(Ⅱ)依题意直线的斜率存在,设直线l的方程为:y-2=k(x-1)(k<0),则
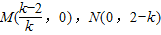
,所以
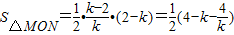
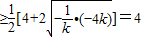
,
当且仅当k=-2时取等号,所以(S
△AOB)
min=4,此时直线l的方程是2x+y-4=0.
点评:本题是中档题,考查三角形面积的最小值的求法,基本不等式的应用,考查计算能力,转化思想的应用.

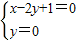 求出A点坐标,根据两直线垂直的条件求出BC、AB所在的直线方程,然后解方程组
求出A点坐标,根据两直线垂直的条件求出BC、AB所在的直线方程,然后解方程组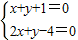 得B的坐标;
得B的坐标;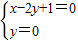 得A(-1,0).
得A(-1,0).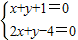 得B(5,-6),
得B(5,-6),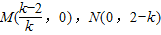 ,所以
,所以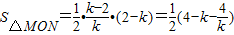
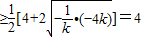 ,
,

 科学实验活动册系列答案
科学实验活动册系列答案