
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2﹣xlna(a>0且a≠1)
(1)求函数f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)单调区间;
(3)若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1(e是自然对数的底数),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥A﹣BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形. 
(1)求证:BC⊥平面APC;
(2)若BC=3,AB=10,求三棱锥B﹣MDC的体积VB﹣MDC .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x
(1)试求函数F(x)=f(x)+f(2x),x∈(﹣∞,0]的最大值;
(2)若存在x∈(﹣∞,0),使|af(x)﹣f(2x)|>1成立,试求a的取值范围;
(3)当a>0,且x∈[0,15]时,不等式f(x+1)≤f[(2x+a)2]恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象如图,
图象如图,![]() 是
是![]() 的导函数,则下列数值排序正确的是( )
的导函数,则下列数值排序正确的是( )
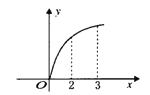
A. ![]()
B. ![]()
C. ![]()
D. ![]()
【答案】C
【解析】结合函数的图像可知过点![]() 的切线的倾斜角最大,过点
的切线的倾斜角最大,过点![]() 的切线的倾斜角最小,又因为点
的切线的倾斜角最小,又因为点![]() 的切线的斜率
的切线的斜率![]() ,点
,点![]() 的切线斜率
的切线斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,故
,故![]() ,应选答案C。
,应选答案C。
点睛:本题旨在考查导数的几何意义与函数的单调性等基础知识的综合运用。求解时充分借助题设中所提供的函数图形的直观,数形结合进行解答。先将经过两切点![]() 的直线绕点
的直线绕点![]() 逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点
逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点![]() 顺时针旋转到与函数的图像相切,这个过程很容易发现
顺时针旋转到与函数的图像相切,这个过程很容易发现![]() ,从而将问题化为直观图形的问题来求解。
,从而将问题化为直观图形的问题来求解。
【题型】单选题
【结束】
9
【题目】已知![]() 、
、![]() 为双曲线
为双曲线![]() :
:![]() 的左、右焦点,点
的左、右焦点,点![]() 在
在![]() 上,
上,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=0,an+1=an+2 ![]() +1
+1
(1)求证数列{ ![]() }是等差数列,并求出an的通项公式;
}是等差数列,并求出an的通项公式;
(2)若bn= ![]() ,求数列{b}的前n项的和Tn .
,求数列{b}的前n项的和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 ![]() . (Ⅰ)求圆C的普通方程和直线l的直角坐标方程;
. (Ⅰ)求圆C的普通方程和直线l的直角坐标方程;
(Ⅱ)设M是直线l上任意一点,过M做圆C切线,切点为A、B,求四边形AMBC面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com