
【题目】如图,三棱锥![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
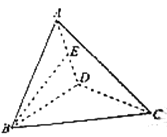
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() ,
,![]() .
.
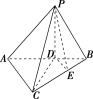
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角.
所成的锐二面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区不同身高![]() 的未成年男性的体重平均值
的未成年男性的体重平均值![]() 如下表:
如下表:
身高x(cm) | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
体重y(kg) | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(Ⅰ)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(Ⅱ)若体重超过相同身高男性体重平均值的![]() 倍为偏胖,低于
倍为偏胖,低于![]() 倍为偏瘦,那么这个地区一名身高
倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]()
![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]()
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,某地认真贯彻落实中央十九大精神和各项宏观调控政策,经济运行平稳增长,民生保障持续加强,惠民富民成效显著,城镇居民收入稳步增长,收入结构稳中趋优.据当地统计局公布的数据,现将8月份至12月份当地的人均月收入增长率与人均月收入分别绘制成折线图(如图一)与不完整的条形统计图(如图二).请从图中提取相关的信息:
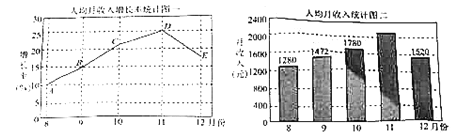
①10月份人均月收入增长率为![]() 左右;
左右;
②11月份人均月收入为2047元;
③从上图可知该地9月份至12月份人均月收入比8月份人均月收入均得到提高.
其中正确的信息个数为( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,
,![]() 为
为![]() 内一点,若分别满足下列四个条件:
内一点,若分别满足下列四个条件:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
则点![]() 分别为
分别为![]() 的( )
的( )
A.外心、内心、垂心、重心B.内心、外心、垂心、重心
C.垂心、内心、重心、外心D.内心、垂心、外心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com