
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 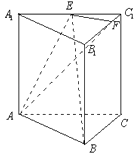
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
【答案】
(1)证明:取B1C1的中点G,连结A1G,
∵B1F=3FC1,FG=FC1,∴EF∥A1G,
在等边△A1B1C1中,由G是B1C1的中点,知A1G⊥B1C1,
∴EF⊥B1C1,
∵三棱柱ABC﹣A1B1C1是直棱柱,∴BB1⊥平面A1B1C1,
又∵EF平面A1B1C1,∴BB1⊥EF,
∵BB1∩B1C1=B1,∴EF⊥平面BB1C1C,
又EF平面AEF,∴平面AEF⊥平面BB1C1C

(2)解:(2)以A为坐标原点,以AA1,AC分别为y轴,z轴,建立空间直角坐标系,
设直三棱柱ABC﹣A1B1C1的棱均为2,则A(0,0,0),B( ![]() ),E(0,1,2),
),E(0,1,2),
∴ ![]() =(0,1,2),
=(0,1,2), ![]() =(
=( ![]() ),
),
设 ![]() =(x,y,z)是平面ABE的一个法向量,
=(x,y,z)是平面ABE的一个法向量,
由 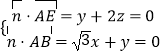 ,取x=﹣2,得
,取x=﹣2,得 ![]() =(﹣2,2
=(﹣2,2 ![]() ,﹣
,﹣ ![]() ),
),
平面AEC1的一个法向量 ![]() =(1,0,0),
=(1,0,0),
设二面角C1﹣AE﹣B的平面角为θ,
则cosθ= ![]() =
= ![]() .
.
∴二面角C1﹣AE﹣B的余弦值为 ![]() .
.

【解析】(1)取B1C1的中点G,连结A1G,推导出EF∥A1G,A1G⊥B1C1 , 从而EF⊥B1C1 , 由三棱柱ABC﹣A1B1C1是直棱柱,得到BB1⊥EF,从而EF⊥平面BB1C1C,由此能证明平面AEF⊥平面BB1C1C.(2)以A为坐标原点,以AA1 , AC分别为y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角C1﹣AE﹣B的余弦值.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,在下列命题中,其中正确命题的序号是.
,在下列命题中,其中正确命题的序号是.
⑴曲线 ![]() 必存在一条与
必存在一条与 ![]() 轴平行的切线;
轴平行的切线;
⑵函数 ![]() 有且仅有一个极大值,没有极小值;
有且仅有一个极大值,没有极小值;
⑶若方程 ![]() 有两个不同的实根,则
有两个不同的实根,则 ![]() 的取值范围是
的取值范围是 ![]() ;
;
⑷对任意的 ![]() ,不等式
,不等式 ![]() 恒成立;
恒成立;
⑸若 ![]() ,则
,则 ![]() ,可以使不等式
,可以使不等式 ![]() 的解集恰为
的解集恰为 ![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有六间不同的电脑室,每天晚上至少开放两间,欲求不同安排方案的种数,现有3位同学分别给出了下列三个结果:① ![]() ;②26-7;③
;②26-7;③ ![]() ,其中正确的结论是( )
,其中正确的结论是( )
A.仅有①
B.仅有②
C.②与③
D.仅有③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a3=9,且an=an﹣1+λn﹣1(n≥2).
(1)求λ的值及数列{an}的通项公式;
(2)设 ![]() ,且数列{bn}的前n项和为Sn , 求S2n .
,且数列{bn}的前n项和为Sn , 求S2n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表: 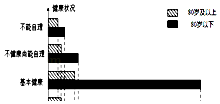
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f (x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 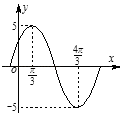
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com