
【题目】已知数列![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() ,其中
,其中![]() .
.
(1)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)设![]() (
(![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
科目:高中数学 来源: 题型:
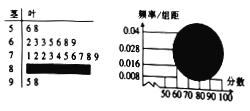
【题目】如图,某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分,据此解答如下问题:
(1)求该班全体男生的人数及分数在![]() 之间的男生人数;
之间的男生人数;
(2)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表);
(3)从分数在![]() 中抽取两个男生,求抽取的两男生分别来自
中抽取两个男生,求抽取的两男生分别来自![]() 、
、![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,且函数
,且函数![]() 的最小正周期为
的最小正周期为![]() 。
。
(1)若函数![]() 在
在![]() 处取到最小值
处取到最小值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)若将函数![]() 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),再将向左平移
倍(纵坐标不变),再将向左平移![]() 个单位,得到的函数图象关于
个单位,得到的函数图象关于![]() 轴对称,求函数
轴对称,求函数![]() 的单调递增区间。
的单调递增区间。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表
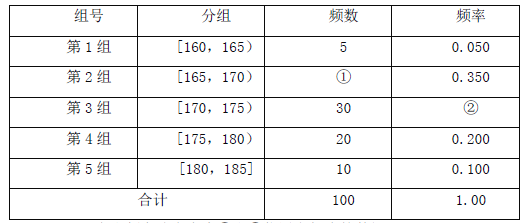
(Ⅰ)求出频率分布表中①和②位置上相应的数据;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5 组中用分层抽样的方法抽取6 名学生进行体能测试,求第3,4,5 组每组各应抽取多少名学生进行测试;
(Ⅲ)在(Ⅱ)的前提下,学校决定在6 名学生中随机抽取2 名学生进行引体向上测试,求第4 组中至少有一名学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的方程
的方程![]() 为抛物线
为抛物线![]() 上一点,
上一点,![]() 为抛物线的焦点.
为抛物线的焦点.
(I)求![]() ;
;
(II)设直线![]() 与抛物线
与抛物线![]() 有唯一公共点
有唯一公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,试问,在坐标平面内是否存在点
,试问,在坐标平面内是否存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是![]() ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是![]() ,甲、乙两台机床加工的零件都是一等品的概率是
,甲、乙两台机床加工的零件都是一等品的概率是![]() .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】7人站成一排.(写出必要的过程,结果用数字作答)
(1)甲、乙两人相邻的排法有多少种?
(2)甲、乙两人不相邻的排法有多少种?
(3)甲、乙、丙三人两两不相邻的排法有多少种?
(4)甲、乙、丙三人至多两人不相邻的排法有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com