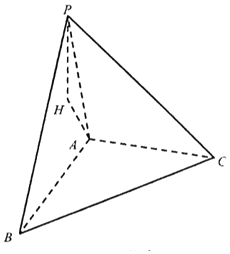
【题目】在三棱锥
中，
，H为P点在平面ABC的投影
，
．
Ⅰ
证明：
平面PHA；
Ⅱ求AC与平面PBC所成角的正弦值．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】下列命题中，正确的个数是__________.（1）已知
，则“
”是“
”的充分不必要条件；（2）已知，则“
”是“
”的必要不充分条件；（3）命题“p或q”为真命题，则“命题p”和“命题q”均为真命题；（4）命题“若
，则
”的逆否命题是真命题.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知四棱锥中
，底面
为菱形，
，
平面，
、
分别是
、
上的中点，直线
与平面
所成角的正弦值为
，点
在
上移动.
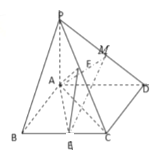
（Ⅰ）证明：无论点在上如何移动，都有平面
平面；
（Ⅱ）求点恰为的中点时，二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解某地区足球特色学校的发展状况，某调查机构得到如下统计数据：
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y（百个） | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（1）根据上表数据，计算y与x的相关系数r，并说明y与x的线性相关性强弱（已知：
则认为
与
线性相关性很强；
，则认为与线性相关性一般，
，则认为y与x线性相关性较弱）
（2）求y与x的线性回归方程，并预测该地区2019年足球特色学校的个数（精确到个位）
参考公式：
；
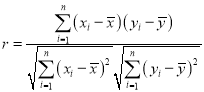
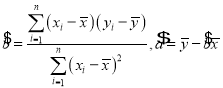
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过直线2x+y+4=0和圆x2+y2+2x﹣4y+1=0的交点，且面积最小的圆方程为（ ）
A.(x+
)2+(y+
)2=
B.(x﹣)2+(y﹣)2=
C.(x﹣)2+(y+)2=D.(x+)2+(y﹣)2=
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，曲线
的参数方程为
，
为参数
，在以坐标原点O为极点，x轴正半轴为极轴的极坐标系中，曲线
的极坐标方程为
．
求曲线的极坐标方程和曲线的直角坐标方程；
若射线l：
与曲线，的交点分别为A，
B异于原点，求
的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
