
【题目】已知点![]() ,抛物线
,抛物线![]() 上存在一点M,使得直线AM的斜率的最大值为1,圆Q的方程为
上存在一点M,使得直线AM的斜率的最大值为1,圆Q的方程为![]() .
.
(1)求点M的坐标和C的方程;
(2)若直线l交C于D,E两点且直线MD,ME都与圆Q相切,证明直线l与圆Q相离.
【答案】(1)![]() ,C的方程为
,C的方程为![]() (2)证明见解析;
(2)证明见解析;
【解析】
(1)(法一)设![]() ,代入抛物线方程,求出直线AM的斜率表达式,利用基本不等式求出
,代入抛物线方程,求出直线AM的斜率表达式,利用基本不等式求出![]() 取得最大值1.解得
取得最大值1.解得![]() ,求出抛物线方程. (法二):设
,求出抛物线方程. (法二):设![]() ,则点
,则点![]() 在x轴上方,直线AM的方程为y=x+1,联立直线AM和抛物线C的方程并整理得
在x轴上方,直线AM的方程为y=x+1,联立直线AM和抛物线C的方程并整理得![]() ,利用判别式解得p,然后求解抛物线方程.
,利用判别式解得p,然后求解抛物线方程.
(2)(法一)求出圆Q的圆心为![]() ,半径为
,半径为![]() ,设过点M的直线MA或MB的方程为
,设过点M的直线MA或MB的方程为![]() 利用点到直线的距离解得
利用点到直线的距离解得![]() .得到直线MD的方程,将直线MD方程与抛物线
.得到直线MD的方程,将直线MD方程与抛物线![]() 方程联立,设
方程联立,设![]() ,求出D,E坐标,推出l的方程
,求出D,E坐标,推出l的方程![]() ,判断直线l与圆Q相离.
,判断直线l与圆Q相离.
(法二)求出圆心Q![]() ,半径为
,半径为![]() .设l的方程为
.设l的方程为![]() .代入抛物线方程,转化求解直线
.代入抛物线方程,转化求解直线![]() 的斜率,直线
的斜率,直线![]() 的方程式,通过
的方程式,通过![]() 与圆Q相切,转化求解D、E坐标,得到直线l得方程判断圆心Q到直线l的距离,得到结果.
与圆Q相切,转化求解D、E坐标,得到直线l得方程判断圆心Q到直线l的距离,得到结果.
解:(1)(法一)设![]() ,则
,则![]() ,
,
由已知可得![]() ,直线AM的斜率为
,直线AM的斜率为
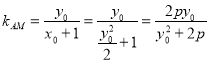
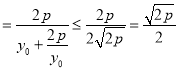
当且仅当![]() 时,
时,![]() 取得最大值1.
取得最大值1.
∴![]() ,解得
,解得![]() ,
,![]()
∴![]() ,C的方程为
,C的方程为![]() .
.
法二:设![]() ,则点M在x轴上方
,则点M在x轴上方
由已知,当直线AM的斜率为1时,直线AM与抛物线C相切
此时直线AM的方程为![]() ,
,
联立直线AM和抛物线C的方程并整理得
![]() ,∴
,∴![]() ,
,
解得:![]() ,且
,且![]()
∴![]() ,C的方程为
,C的方程为![]() .
.
(2)(法一)圆Q的方程可化为![]()
圆Q的圆心为![]() ,半径为
,半径为![]() ,
,
设过点M的直线MA或MB的方程为![]()
化为![]() ,则
,则![]() ,解得
,解得![]() .
.
不妨设直线MD的方程为![]() ,
,
将直线MD与抛物线![]() 方程联立
方程联立
消去x得![]() .
.
设![]() ,则
,则![]()
∴![]() ,
,![]()
同理设![]() ,
,![]() .
.
∴![]() ,
,![]()
∴直线l的斜率![]()
∴直线l的方程为![]() ,即
,即![]()
∴l的方程![]() ,
,
此时圆心Q到直线l的距离![]()
∴直线l与圆Q相离
(法二)圆Q的方程可化为![]() .
.
圆心![]() ,半径为
,半径为![]() .
.
由题知,直线l的斜率必存在,
设l的方程为![]() .
.
联立![]() ,消去x得
,消去x得![]()
由![]() ,得
,得![]() ,①
,①
设![]()
则![]() ,
,![]() ,②
,②
直线MD的斜率为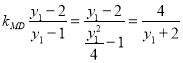
直线MD的方程式为![]() ,
,
即![]()
∵MD与圆Q相切,∴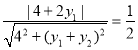
∴![]() ,∴
,∴![]()
由题知:![]() ,
,![]()
或![]() ,
,![]()
代入②得![]() ,
,![]()
∴![]() ,满足①式,
,满足①式,
∴直线l得方程为![]() ,即
,即![]() .
.
此时圆心Q到直线l的距离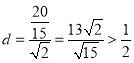 .
.
∴直线l与圆Q相离.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
【题目】下表是某原料在市场上从2013年至2019年这7年中每年的平均价格(单位:千元/吨)数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
平均价格 (单位:千元/吨) |
|
|
|
|
|
|
|
(![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程(系数精确到
为预报变量的线性回归方程(系数精确到![]() );
);
(2)以(1)的结论为依据,预测2032年该原料价格.预估该原料价格在哪一年突破1万元/吨?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: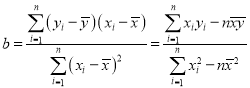 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,且存在常数
,且存在常数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,则称数列
,则称数列![]() 为“k控数列”.
为“k控数列”.
(1)若公差为d的等差数列![]() 是“2控数列”,求d的取值范围;
是“2控数列”,求d的取值范围;
(2)已知公比为![]() 的等比数列
的等比数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 与
与![]() 都是“k控数列”,求q的取值范围(用k表示).
都是“k控数列”,求q的取值范围(用k表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(3)判断数列![]() 中是否存在三项成等差数列,并证明你的结论.
中是否存在三项成等差数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是( )
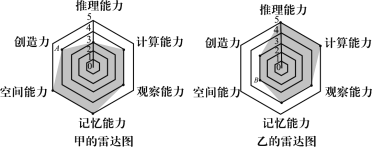
A.甲的六大能力中推理能力最差B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力D.乙的六大能力整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出![]() 、
、![]() 两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于
两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于![]() 时为废品,指标值在
时为废品,指标值在![]() 为一等品,大于
为一等品,大于![]() 为特等品.现把测量数据整理如下,其中
为特等品.现把测量数据整理如下,其中![]() 配方废品有
配方废品有![]() 件.
件.
![]() 配方的频数分布表
配方的频数分布表
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)求![]() ,
,![]() 的值;
的值;
(2)试确定![]() 配方和
配方和![]() 配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绿水青山就是金山银山.某山村为做好水土保持,退耕还林,在本村的山坡上种植水果,并推出山村游等旅游项目.为预估今年7月份游客购买水果的情况,随机抽样统计了去年7月份100名游客的购买金额.分组如下:![]() ,
,![]() ,
,![]()
![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
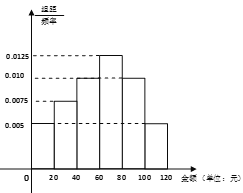
(1)请用抽样的数据估计今年7月份游客人均购买水果的金额(同一组中的数据用该组区间中点作代表).
(2)若把去年7月份购买水果不低于80元的游客,称为“水果达人”. 填写下面列联表,并根据列联表判断是否有95%的把握认为“水果达人”与性别有关系?
水果达人 | 非水果达人 | 合计 | |
男 | 10 | ||
女 | 30 | ||
合计 |
(3)为吸引顾客,商家特推出两种促销方案.方案一:每满80元可立减10元;方案二:金额超过80元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
附:参考公式和数据:![]() ,
,![]() .临界值表:
.临界值表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个人到![]() ,
,![]() ,
,![]() 三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到
三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到![]() 景点的方案有( )
景点的方案有( )
A.18种B.12种C.36种D.24种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com