练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    平面上两条直线x-2y+1=0，x+ky=0，如果这两条直线将平面划分为三部分，则实数k的取值为________．

    -2
    分析：由题意可得这两条直线互相平行，故它们的斜率相等，即 =，由此解得k的值．
    解答：∵平面上两条直线x-2y+1=0和x+ky=0 将平面划分为三部分，故这两条直线互相平行，
    ∴它们的斜率相等，即 =，解得 k=-2，
    故答案为-2．
    点评：本题主要考查两直线平行的性质，两直线平行，斜率相等，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，平面中两条直线l1和l 2相交于点O，对于平面上任意一点M，若x，y分别是M到直线l 1和l 2的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
    ①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
    ②若pq=0，且p+q≠0，则“距离坐标”为（ p，q） 的点有且只有2个；
    ③若pq≠0则“距离坐标”为 （ p，q） 的点有且只有3个．
    上述命题中，正确的有
    ①②
    ①②
    ．（填上所有正确结论对应的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若x，y分别是M到直线l1和l2的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
    ①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
    ②若pq=0，且p+q≠0，则“距离坐标”为（p，q） 的点有且只有2个；
    ③若pq≠0则“距离坐标”为 （p，q） 的点有且只有4个．
    上述命题中，正确命题的是
    ①②③
    ①②③
    ．（写出所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    平面上两条直线x-2y+1=0，x+ky=0，如果这两条直线将平面划分为三部分，则实数k的取值为
    -2
    -2
    ．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省济宁市汶上一中高二12月质检理科数学试卷（带解析） 题型：填空题

    如图，平面中两条直线l 1 和l 2相交于点O，对于平面上任意一点M，若x , y分别是M到直线l1和l2的距离，则称有序非负实数对（x , y）是点M的“ 距离坐标” 。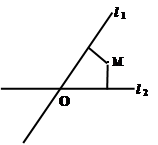

    已知常数p≥0, q≥0，给出下列三个命题：
    ①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
    ②若pq="0," 且p+q≠0，则“距离坐标”为( p, q) 的点有且只有2个；
    ③若pq≠0则“距离坐标”为( p, q) 的点有且只有4个.
    上述命题中，正确命题的是           ．   （写出所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省济宁市高二12月质检理科数学试卷（解析版） 题型：填空题

    如图，平面中两条直线l 1 和l 2相交于点O，对于平面上任意一点M，若x , y分别是M到直线l1和l2的距离，则称有序非负实数对（x , y）是点M的“ 距离坐标” 。

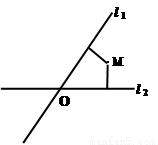
    已知常数p≥0, q≥0，给出下列三个命题：

    ①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；

    ②若pq="0," 且p+q≠0，则“距离坐标”为( p, q) 的点有且只有2个；

    ③若pq≠0则“距离坐标”为( p, q) 的点有且只有4个.

    上述命题中，正确命题的是           ．   （写出所有正确命题的序号）

     

    查看答案和解析>>

    同步练习册答案