
【题目】已知函数![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得
,使得![]() 的解集恰好是
的解集恰好是![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)符合要求的整数
;(2)符合要求的整数![]() 是
是 或
或 .
.
【解析】试题分析:(1)求出函数的对称轴,由于y=|f(x)|在[﹣1,0]上是减函数,则讨论区间在对称轴的右边,且f(0)不小于0,区间在对称轴的左边,且f(0)不大于0.解出它们即可;
(2)假设存在整数a,b,使得a≤f(x)≤b的解集恰好是[a,b].则f(a)=a,f(b)=a,a≤f(![]() )≤b,由f(a)=f(b)=a,解出整数a,b,再代入不等式检验即可.
)≤b,由f(a)=f(b)=a,解出整数a,b,再代入不等式检验即可.
试题解析:
(1)令![]() ,则
,则![]() .
.
当![]() ,即
,即![]() 时,
时, ![]() 恒成立,
恒成立,
所以![]() .
.
因为![]() 在
在![]() 上是减函数,
上是减函数,
所以![]() ,解得
,解得![]() ,
,
所以![]() .
.
由![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时, ![]() 的图象对称轴
的图象对称轴![]() ,
,
且方程![]() 的两根均为正,
的两根均为正,
此时![]() 在
在![]() 为减函数,所以
为减函数,所以![]() 符合条件.
符合条件.
当![]() 时,
时, ![]() 的图象对称轴
的图象对称轴![]() ,
,
且方程![]() 的根为一正一负,
的根为一正一负,
要使![]() 在
在![]() 单调递减,则
单调递减,则![]() ,解得
,解得![]() .
.
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.
(2)假设存在整数![]() ,使
,使![]() 的解集恰好是
的解集恰好是![]() ,则
,则
①若函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
, ![]() 且
且![]() ,
,
即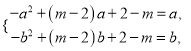
作差得到![]() ,代回得到:
,代回得到: ![]() ,即
,即![]() ,由于
,由于![]() 均为整数,
均为整数,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,经检验均不满足要求;
,经检验均不满足要求;
②若函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,
, ![]() 且
且![]() ,
,
即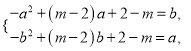
作差得到![]() ,代回得到:
,代回得到: ![]() ,即
,即![]() ,由于
,由于![]() 均为整数,
均为整数,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,经检验均不满足要求;
,经检验均不满足要求;
③若函数![]() 在
在![]() 上不单调,则
上不单调,则![]() ,
, ![]() 且
且![]() ,
,
即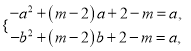 作差得到
作差得到![]() ,代回得到:
,代回得到: ![]() ,即
,即![]() ,由于
,由于![]() 均为整数,
均为整数,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,,经检验均满足要求;
,,经检验均满足要求;
综上,符合要求的整数![]() 是
是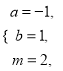 或
或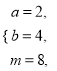


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2﹣3x(a,b∈R)在点(1,f(1))处的切线方程为y+2=0.
(1)求函数f(x)的解析式;
(2)若对于区间[﹣2,2]上任意两个自变量的值x1 , x2都有|f(x1)﹣f(x2)|≤c,求实数c的最小值;
(3)若过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() (a>0)
(a>0)
(1)若函数f(x)在x=2处的切线与x轴平行,求实数a的值;
(2)讨论函数f(x)在区间[1,2]上的单调性;
(3)证明: ![]() >e.
>e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是
是![]() 直径,
直径, ![]() 所在的平面,
所在的平面, ![]() 是圆周上不同于
是圆周上不同于![]() 的动点.
的动点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,且当二面角
,且当二面角![]() 的正切值为
的正切值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:①
点,则翻折后的几何体中有如下描述:①![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;②
;②![]() ;③
;③![]() ;④平面
;④平面![]() 平面
平面![]() ,其中正确的命题序号为___________.
,其中正确的命题序号为___________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集R中定义一种运算“*”,对任意给定的a,b∈R,a*b为唯一确定的实数,且具有性质: ⑴对任意a,b∈R,a*b=b*a;(2)对任意a∈R,a*0=a;(3)对任意a,b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.关于函数f(x)=(3x)* ![]() 的性质,有如下说法:
的性质,有如下说法:
①函数f(x)的最小值为3;
②函数f(x)为奇函数;
③函数f(x)的单调递增区间为(﹣∞,﹣ ![]() ),(
),( ![]() ,+∞).
,+∞).
其中所有正确说法的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元?
(2)当一次订购量为![]() 个, 每件商品的实际批发价为
个, 每件商品的实际批发价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(3)根据市场调查发现,经销商一次最大定购量为![]() 个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com