分析:(1)先根据其为正方体得到∠C1AB1就是AC1与平面AA1B1B所成的角;然后在RT△C1AB1中求其正切即可;
(2)先过B1作B1E⊥BC1于E,过E作EF⊥AC1于F,连接B1F;根据AB⊥平面B1C1CB推得B1E⇒AC1;进而得到∠B1FE是二面角B-AC1-B1的平面角;然后通过求三角形的边长得到二面角B-AC1-B1的大小即可.
解答:
解:(1)连接AB
1,∵ABCD-A
1B
1C
1D
1是正方体
∴B
1C
1⊥平面ABB
1A
1,AB
1是AC
1在平面AA
1B
1B上的射影
∴∠C
1AB
1就是AC
1与平面AA
1B
1B所成的角
在RT△C
1AB
1中,tan∠C
1AB
1=
=
∴直线AC
1与平面AA
1B
1B所成的角的正切值为
(2)过B
1作B
1E⊥BC
1于E,过E作EF⊥AC
1于F,连接B
1F;
∵AB⊥平面B
1C
1CB,⇒AB⊥B
1E⇒B
1E⇒平面ABC
1⇒B
1E⇒AC
1∴∠B
1FE是二面角B-AC
1-B
1的平面角
在RT△BB
1C
1中,B
1E=C
1E=
BC
1=
,
在RT△ABC
1中,sin∠BC
1A=
=
∴EF=C
1E•sin∠BC
1A=
,
∴tan∠B
1FE=
=
∴∠B
1FE=60°,即二面角B-AC
1-B
1的大小为60°.
点评:本题主要考察线面角以及二面角的平面角及其求法.解决二面角的平面角及求法的关键在于把二面角的平面角找出来或做出来,常用的做法是三垂线法.

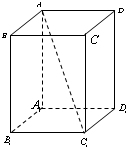 已知ABCD-A1B1C1D1是边长为1的正方体,求:
已知ABCD-A1B1C1D1是边长为1的正方体,求: 解:(1)连接AB1,∵ABCD-A1B1C1D1是正方体
解:(1)连接AB1,∵ABCD-A1B1C1D1是正方体

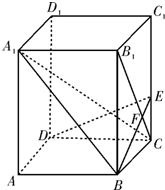 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,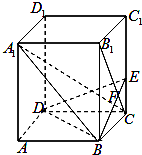 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.