
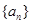 、
、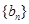 满足
满足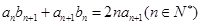 .
.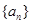 是常数列(各项都相等的数列),且
是常数列(各项都相等的数列),且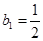 时,求数列
时,求数列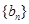 的通项公式;
的通项公式;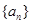 、
、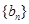 都是公差不为0的等差数列,求证:数列
都是公差不为0的等差数列,求证:数列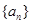 有无穷多个,而数列
有无穷多个,而数列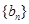 惟一确定;
惟一确定;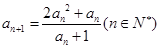 ,
,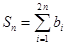 ,求证:
,求证: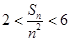 .
. ;(Ⅱ)详见解析;(Ⅲ)详见解析.
;(Ⅱ)详见解析;(Ⅲ)详见解析.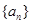 是常数列,得
是常数列,得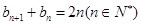 ,进而探求数列项间的关系;(Ⅱ)将等差数列
,进而探求数列项间的关系;(Ⅱ)将等差数列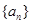 、
、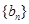 的通项公式代入
的通项公式代入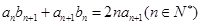 ,根据等式恒成立,求首项和公差;(Ⅲ)利用题中所给关系式对
,根据等式恒成立,求首项和公差;(Ⅲ)利用题中所给关系式对 进行适当放缩,求出上界和下界.
进行适当放缩,求出上界和下界.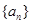 是常数列,且
是常数列,且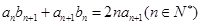 ,所以
,所以 ①,因此
①,因此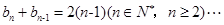 ②,①-②得,
②,①-②得, ,这说明数列
,这说明数列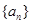 的序号为奇数的项及序号为偶数的项均按原顺序组成公差为2的等差数列,又
的序号为奇数的项及序号为偶数的项均按原顺序组成公差为2的等差数列,又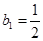 ,
,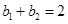 ,所以
,所以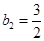 ,因此
,因此 ,
,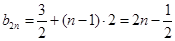 ,即
,即 .
.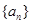 、
、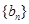 都是公差分别为
都是公差分别为 ,将其通项公式代入
,将其通项公式代入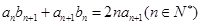 得
得 ,因为它是恒等式,所以
,因为它是恒等式,所以 ,解得
,解得 ,因此
,因此 .
. 可以取无穷多非零的实数,故数列
可以取无穷多非零的实数,故数列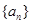 有无穷多个,而数列
有无穷多个,而数列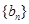 惟一确定;
惟一确定;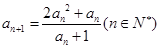 ,且
,且 ,所以
,所以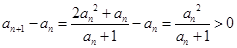 ,即
,即 ,所以
,所以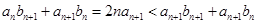 ,得
,得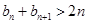 ,因此
,因此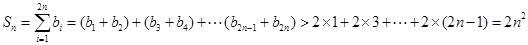 .
. 得,
得, ,而
,而 ,所以
,所以 ,因此
,因此 ,所以
,所以 ,所以
,所以 .
.

科目:高中数学 来源:不详 题型:解答题
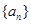 的各项均为正数,
的各项均为正数,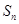 为其前
为其前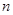 项和,对于任意的
项和,对于任意的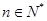 ,满足关系式
,满足关系式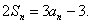
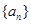 的通项公式;
的通项公式;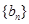 的通项公式是
的通项公式是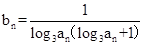 ,前
,前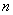 项和为
项和为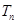 ,求证:对于任意的正整数
,求证:对于任意的正整数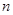 ,总有
,总有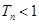 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
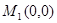 ,
,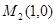 .以
.以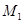 为圆心,
为圆心,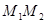 为半径作圆交
为半径作圆交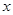 轴于点
轴于点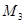 (异于
(异于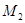 ),记作⊙
),记作⊙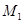 ;以
;以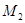 为圆心,
为圆心,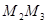 为半径作圆交
为半径作圆交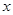 轴于点
轴于点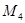 (异于
(异于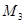 ),记作⊙
),记作⊙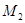 ;……;以
;……;以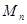 为圆心,
为圆心,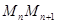 为半径作圆交
为半径作圆交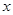 轴于点
轴于点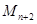 (异于
(异于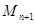 ),记作⊙
),记作⊙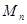 .当
.当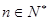 时,过原点作倾斜角为
时,过原点作倾斜角为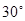 的直线与⊙
的直线与⊙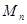 交于
交于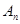 ,
,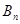 .考察下列论断:
.考察下列论断: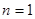 时,
时,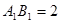 ;当
;当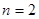 时,
时,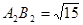 ;当
;当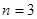 时,
时,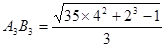 ;当
;当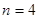 时,
时,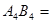 .
.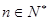 ,
,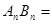 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.8年 | B.10年 | C.12年 | D.15年 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com