
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
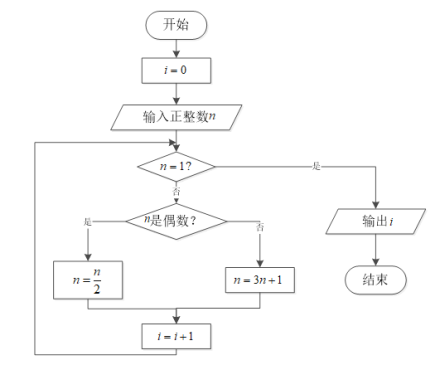
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】2014年非洲爆发了埃博拉病毒疫情,在疫情结束后,当地防疫部门做了一项回访调查,得到如下结果,
患病 | 不患病 | |
有良好卫生习惯 | 20 | 180 |
无良好卫生习惯 | 80 | 220 |
(1)结合上面列联表,是否有![]() 的把握认为是否患病与卫生习惯有关?
的把握认为是否患病与卫生习惯有关?
(2)现从有良好卫生习惯且不患病的180人中抽取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共5人,再从这5人中选两人给市民做健康专题报告,求
共5人,再从这5人中选两人给市民做健康专题报告,求![]() ,
,![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
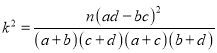
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sinx(sinx![]() cosx)﹣1图象向右平移
cosx)﹣1图象向右平移![]() 个单位得函数g(x)的图象,则下列命题中正确的是( )
个单位得函数g(x)的图象,则下列命题中正确的是( )
A.f(x)在(![]() ,
,![]() )上单调递增
)上单调递增
B.函数f(x)的图象关于直线x![]() 对称
对称
C.g(x)=2cos2x
D.函数g(x)的图象关于点(![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
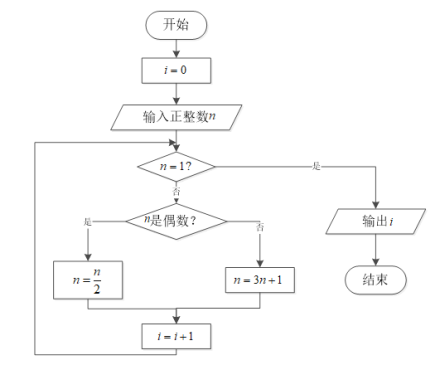
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论:
①下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的![]() ,
,![]() 分别为8,12,则输出的
分别为8,12,则输出的![]() ;
;

②若用样本数据0,-1,2,3来估计总体的标准差,则总体的标准差估计值为![]() ;
;
③命题:“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
④已知正数![]() ,
,![]() 满足
满足![]() ,则
,则![]() 的最大值是
的最大值是![]() ;
;
⑤已知函数![]() 满足
满足![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() .则
.则![]() 在区间
在区间![]() 为增函数.
为增函数.
其中结论正确的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com