
【题目】已知函数![]() ,若在区间
,若在区间![]() 内有且只有一个实数
内有且只有一个实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(1)判断函数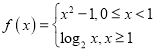 在区间
在区间![]() 内是否具有唯一零点,说明理由:
内是否具有唯一零点,说明理由:
(2)已知向量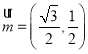 ,
,![]() ,
,![]() ,证明
,证明![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(3)若函数![]() 在区间
在区间![]() 内具有唯一零点,求实数
内具有唯一零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)是,详见解析(2)证明见解析(3)![]()
【解析】
(1)利用分段函数,分类讨论函数的单调性,从而得出结论;
(2)两个向量的数量积共公式以及三角恒等变换,化简![]() 的解析式,再利用正弦函数的性质得出结论;
的解析式,再利用正弦函数的性质得出结论;
(3)利用二次函数的性质,分类讨论,求得![]() 的范围.
的范围.
(1)函数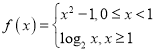 在区间
在区间![]() 内具有唯一零点,理由如下:
内具有唯一零点,理由如下:
当![]() 时,有
时,有![]() ,且当
,且当![]() 时,有
时,有![]() ;
;
当![]() 时,
时,![]() 是增函数,有
是增函数,有![]() ,
,
故函数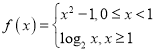 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(2)由向量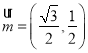 ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
令![]() ,
,![]() ,解得
,解得![]() ,
,
所以函数![]() 在区间
在区间![]() 内具有唯一零点
内具有唯一零点![]() ,使得
,使得![]() ,
,
故函数![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(3)由函数![]() 在区间
在区间![]() 内具有唯一零点,该二次函数的对称轴为
内具有唯一零点,该二次函数的对称轴为![]() ,
,
①当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 是增函数,
是增函数,
只需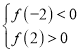 ,即
,即![]() ,解得
,解得![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
②当![]() ,即
,即![]() 时,若使函数
时,若使函数![]() 在区间
在区间![]() 内具有零点,
内具有零点,
则![]() ,解得
,解得![]() 或
或![]() ,
,
所以,![]() ,
,
i当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内具有唯一零点
内具有唯一零点![]() ,即
,即![]() ,符合题意,
,符合题意,
ii当![]() 时,若使函数
时,若使函数![]() 在区间
在区间![]() 内具有唯一零点,只需
内具有唯一零点,只需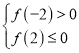 ,
,
即![]() ,解得
,解得![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
③当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 是减函数,
是减函数,
当![]() 时,只需
时,只需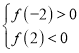 ,即
,即![]() ,解得
,解得![]() ,
,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
所以函数![]() 在区间
在区间![]() 上具有唯一零点
上具有唯一零点![]() ,符合题意,
,符合题意,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
综上所述:实数![]() 的取值范围为
的取值范围为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图是国家统计局给出的2014年至2018年我国城乡就业人员数量的统计图表,结合这张图表,以下说法错误的是( )
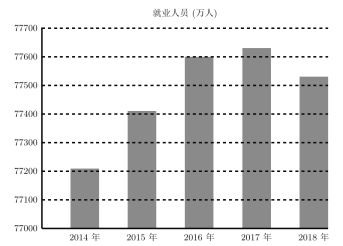
A.2017年就业人员数量是最多的
B.2017年至2018年就业人员数量呈递减状态
C.2016年至2017年就业人员数量与前两年比较,增加速度减缓
D.2018年就业人员数量比2014年就业人员数量增长超过400万人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候
,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候![]() 的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则
的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() ).(参考数据
).(参考数据![]() )
)
A.3.14B.3.11C.3.10D.3.05
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,直线l与椭圆C交于P,Q两点,且点M满足
,直线l与椭圆C交于P,Q两点,且点M满足![]() .
.
(1)若点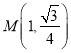 ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线l过点![]() 且不与x轴重合,过点M作垂直于l的直线
且不与x轴重合,过点M作垂直于l的直线![]() 与y轴交于点
与y轴交于点![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点O,焦点在x轴上的椭圆C过点![]() ,F为C的右焦点,⊙F的方程为
,F为C的右焦点,⊙F的方程为![]()
(1)求C的方程;
(2)若直线![]()
![]() 与⊙O相切,与⊙F交于M、N两点,与C交于P、Q两点,其中M、P在第一象限,记⊙O的面积为
与⊙O相切,与⊙F交于M、N两点,与C交于P、Q两点,其中M、P在第一象限,记⊙O的面积为![]() ,求
,求![]() 取最大值时,直线l的方程.
取最大值时,直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,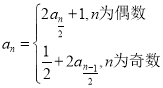 ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(3)对任意的![]() ,
,![]() ,在数列
,在数列![]() 中是否存在连续的
中是否存在连续的![]() 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这![]() 项,并证明这
项,并证明这![]() 项构成等差数列:若不存在,请说明理由.
项构成等差数列:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两城市![]() 和
和![]() 相距
相距![]() ,现计划在两城市外以
,现计划在两城市外以![]() 为直径的半圆
为直径的半圆![]() 上选择一点
上选择一点![]() 建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城
建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城![]() 和城
和城![]() 的总影响度为城
的总影响度为城![]() 和城
和城![]() 的影响度之和,记
的影响度之和,记![]() 点到城
点到城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理场对城
处的垃圾处理场对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() ,统计调查表明:垃圾处理场对城
,统计调查表明:垃圾处理场对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为4,对城
的距离的平方成反比,比例系数为4,对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为
的距离的平方成反比,比例系数为![]() ,当垃圾处理场建在
,当垃圾处理场建在![]() 的中点时,对城
的中点时,对城![]() 和城
和城![]() 的总影响度为0.065;
的总影响度为0.065;
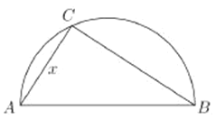
(1)将![]() 表示成
表示成![]() 的函数;
的函数;
(2)判断![]() 上是否存在一点,使建在此处的垃圾处理场对城
上是否存在一点,使建在此处的垃圾处理场对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,说明理由;
的距离;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设![]() 是
是![]() 的反函数.当
的反函数.当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“
是“![]() 数列”.
数列”.
(1)若![]() 是“
是“![]() 数列”,且
数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 是等差数列,首项为
是等差数列,首项为![]() ,公差为
,公差为![]() ,且
,且![]() ,判断
,判断![]() 是否为“
是否为“![]() 数列”;
数列”;
(3)设数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,若数列
,若数列![]() 与
与![]() 都是“
都是“![]() 数列”,求
数列”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com