
【题目】“绿水青山就是金山银山”,“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容,某班在一次研学旅行活动中,为了解某苗圃基地的柏树幼苗生长情况,在这些树苗中随机抽取了120株测量高度(单位:![]() ),经统计,树苗的高度均在区间
),经统计,树苗的高度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于
分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于![]() 的为优质树苗.
的为优质树苗.
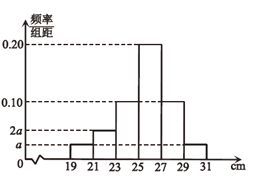
(1)求图中![]() 的值;
的值;
(2)已知所抽取的这120株树苗来自于![]() ,
,![]() 两个试验区,部分数据如列联表:
两个试验区,部分数据如列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
(3)用样本估计总体,若从这批树苗中随机抽取4株,其中优质树苗的株数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:参考公式与参考数据: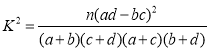 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【答案】(1)![]() ;(2)列联表见解析,没有99.9%的把握认为优质树苗与
;(2)列联表见解析,没有99.9%的把握认为优质树苗与![]() 两个试验区有关系;(3)分布列见解析,
两个试验区有关系;(3)分布列见解析,![]()
【解析】
(1)由频率分布直方图中所有频率(小矩形面积)和为1可求得![]() ;
;
(2)由频率分布直方图求出优质树苗和非优质树苗的株数后可填写列联表,求出![]() 后知有无关系;
后知有无关系;
(3)由(2)知这批树苗为优质树苗的概率为![]() ,
,![]() 的可能取值为0,1,2,3,4,
的可能取值为0,1,2,3,4, ![]() 服从二项分布,即
服从二项分布,即![]() ,计算出各概率,得分布列,根据期望公式计算出期望.
,计算出各概率,得分布列,根据期望公式计算出期望.
(1)根据频率分布直方图数据,有![]()
![]() ,解得:
,解得:![]() .
.
(2)根据频率分布直方图可知,样本中优质树苗棵树有![]()
列联表如下:
|
| 合计 | |
优质树苗 | 10 | 20 | 30 |
非优质树苗 | 60 | 30 | 90 |
合计 | 70 | 50 | 120 |
可得;![]()
![]()
所以,没有99.9%的把握认为优质树苗与![]() 两个试验区有关系
两个试验区有关系
注:也可由![]()
![]() 得出结论
得出结论
(3)用样本估计总体,由题意,这批树苗为优质树苗的概率为![]()
![]() 的可能取值为0,1,2,3,4,由题意知:
的可能取值为0,1,2,3,4,由题意知:![]() 服从二项分布,即
服从二项分布,即![]()
![]()
![]()
即:![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() .
.
![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 数学期望为
数学期望为![]()
(或![]()
![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,点
,点![]() ,若
,若![]() 的内切圆的半径与外接圆的半径的比是
的内切圆的半径与外接圆的半径的比是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的右顶点,设圆
的右顶点,设圆![]() :
:![]() ,不与
,不与![]() 轴垂直的直线
轴垂直的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,原点
两点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,线段
,线段![]() 、
、![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 、
、![]() ,
,![]() ,垂足为
,垂足为![]() .设
.设![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .
.
①试确定![]() 与
与![]() 的关系式;、
的关系式;、
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
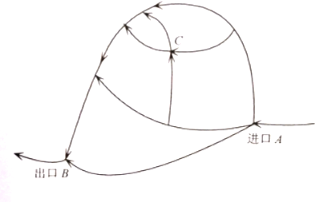
【题目】如图是一旅游景区供游客行走的路线图,假设从进口![]() 开始到出口
开始到出口![]() ,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共
,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共![]() 名游客结伴到旅游景区游玩,他们从进口
名游客结伴到旅游景区游玩,他们从进口![]() 的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口
的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口![]() 集中,设点
集中,设点![]() 是其中的一个交叉路口点.
是其中的一个交叉路口点.
(1)求甲经过点![]() 的概率;
的概率;
(2)设这![]() 名游客中恰有
名游客中恰有![]() 名游客都是经过点
名游客都是经过点![]() ,求随机变量
,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的右焦点为
的右焦点为![]() ,且短轴长为
,且短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
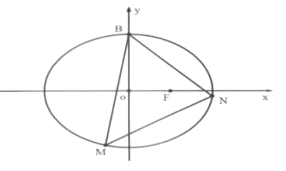
(2)设点![]() 为椭圆
为椭圆![]() 与
与![]() 轴正半轴的交点,是否存在直线
轴正半轴的交点,是否存在直线![]() ,使得
,使得![]() 交椭圆
交椭圆![]() 于
于![]() 两点,且
两点,且![]() 恰是
恰是![]() 的垂心?若存在,求
的垂心?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得![]() 分).设每次击鼓出现音乐的概率为
分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com