
分析 (Ⅰ)由$\frac{{a}_{n+1}-\frac{{2}^{n+2}}{3}}{{a}_{n}-\frac{{2}^{n+1}}{3}}$=$\frac{-{a}_{n}+\frac{{2}^{n+1}}{3}}{{a}_{n}-\frac{{2}^{n+1}}{3}}$=-1.由${a}_{1}-\frac{4}{3}=-\frac{1}{3}$,能证明{${a}_{n}-\frac{{2}^{n+1}}{3}$}是等比数列,由此能求出{an}的通项公式.
(Ⅱ)由bn=3nan=n•2n-1+(-1)n•n,利用分组求和法能求出数列{bn}的前n项和Tn.
解答 证明:(Ⅰ)∵Sn是数列{an}的前n项和,且${a_1}=1,{a_{n+1}}+{a_n}={2^{n+1}}(n∈{N^*})$,
∴$\frac{{a}_{n+1}-\frac{{2}^{n+2}}{3}}{{a}_{n}-\frac{{2}^{n+1}}{3}}$=$\frac{{2}^{n+1}-{a}_{n}-\frac{{2}^{n+2}}{3}}{{a}_{n}-\frac{{2}^{n+1}}{3}}$=$\frac{-{a}_{n}+\frac{{2}^{n+1}}{3}}{{a}_{n}-\frac{{2}^{n+1}}{3}}$=-1.
由${a}_{1}-\frac{4}{3}=-\frac{1}{3}$,得{${a}_{n}-\frac{{2}^{n+1}}{3}$}是首项为-$\frac{1}{3}$,公比为-1的等比数列,
∴${a}_{n}-\frac{{2}^{n+1}}{3}$=-$\frac{1}{3}$(-1)n,
∴an=$\frac{{2}^{n+1}}{3}+\frac{1}{3}(-1)^{n}$.
解:(Ⅱ)bn=3nan=n•2n-1+(-1)n•n,
取{n•2n-1}前n项和An,{(-1)n•n}前n项和Bn,
则${A}_{n}=1•{2}^{2}+2•{2}^{3}+3•{2}^{4}+…+n•{2}^{n+1}$,
2An=1•23+2•24+3•25+…+n•2n+2,
则-An=22+23+24+…+2n+1-n•2n+2
=$\frac{4(1-{2}^{n})}{1-2}-n•{2}^{n+2}$,
∴${A}_{n}=4+(n-1)•{2}^{n+2}$,
当n是奇数时,Bn=(-1)+2+(-3)+4+(-5)+…+(-n)=-$\frac{n+1}{2}$,
当n是偶数时,Bn=(-1)+2+(-3)+4+(-5)+$…+(-n)=\frac{n}{2}$,
∴Tn=$\left\{\begin{array}{l}{4+(n-1)•{2}^{n+2}-\frac{n+1}{2},n是奇数}\\{46(n-1)•{2}^{n+2}+\frac{n}{2},n是偶数}\end{array}\right.$.
点评 本题考查等比数列的证明,考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意分组求和法和错位相减法的合理运用.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 20 | C. | 12 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
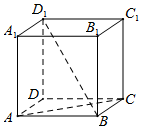 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
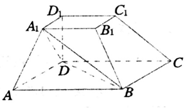 如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com