
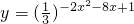 (-3≤x≤1)的值域是________,单调递增区间是________.
(-3≤x≤1)的值域是________,单调递增区间是________. 和t=-2x2-8x+1,两个函数符合而成,第一个函数是一个单调递减函数,要求原函数的值域,只要求出t=-2x2-8x+1,在[1,3]上的值域就可以,再根据同增异减点的单调区间.
和t=-2x2-8x+1,两个函数符合而成,第一个函数是一个单调递减函数,要求原函数的值域,只要求出t=-2x2-8x+1,在[1,3]上的值域就可以,再根据同增异减点的单调区间.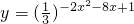
 和t=-2x2-8x+1,两个函数符合而成,
和t=-2x2-8x+1,两个函数符合而成,

 天天向上口算本系列答案
天天向上口算本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com