Question

 

函数f (x)＝x²＋ax＋3，当x∈[－2, 2]时f (x)≥a恒成立，求a的取值范围

 

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

 解：要使函数f (x)＝x²＋ax＋3，当x∈[－2, 2]时f (x)≥a恒成立，即函数f (x)＝x²＋ax＋3在x∈[－2, 2]上的最小值大于等于a. 又f (x)＝(x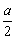＋)²＋3－, x∈[－2, 2],

    ① 当－2≤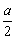－≤2时, 即a∈[－4, 4]时, f (x)的最小值为3－≥a,

∴ a²＋4a－12≤0, 解得－6≤a≤2, ∴－4≤a≤2

    ② 当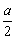－<－2时, 即a>4时，f (x)的最小值为f (－2)＝a≥a,

∴ a≤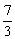与a≥4矛盾.

③ 当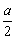－>2时,即a<－4时，f (x)的最小值为f (2)＝7＋2a≥a, ∴ a≥－7,

∴ －7≤a<－4,    综上得  －7≤a≤2.