
分析 利用特殊值代入法,先求出a0+a1+a2+…+a7的值,再求a1+a3+a5+a7的值.
解答 解:(1)∵(2x-1)7=a0+a1x+a2x2+…+a7x7,
令x=1,得(2×1-1)7=a0+a1+a2+…+a7,
∴a0+a1+a2+…+a7=1;
(2)(2x-1)7=a0+a1x+a2x2+…+a7x7中,
令x=-1,得-37=a0-a1+a2+…-a7x7①,
又1=a0+a1+a2+…+a7②;
②-①,得2(a1+a3+a5+a7)=1+37,
∴a1+a3+a5+a7=$\frac{1{+3}^{7}}{2}$.
点评 本题考查了二项式定理的应用问题,也考查了利用特殊值求值的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
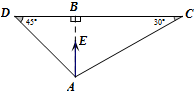 将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.
将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com