练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数的图象经过点（1，1），．

    （1）求函数的解析式；

    （2）判断函数在（0，+）上的单调性并用定义证明；

    （3）求在区间上的值域；

    【答案】（1）（2）函数在（0，+）上为减函数（3）

    【解析】

    试题分析：（1）将点的坐标代入函数式可得到关于的关系式，解方程可求得其值，从而确定函数解析式；（2）判断函数单调性，首先假设，在此基础上判断的大小关系，从而确定单调性；（3）由函数的单调性可确定函数在上的最大值和最小值，从而求得值域

    试题解析：（1） 由 f(x)的图象过A、B，则，解得．

    ∴ ……4分

    （2）证明：设任意x1，x2∈（0，+），且x1<x2．

    ∴

    .

    由x1，x2∈（0，+），得x1x2>0，x1x2+2>0．

    由x1<x2，得．

    ∴，即．

    ∴函数在（0，+）上为减函数．

    （3）函数在（0，+）上为减函数

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知极坐标系的极点在直角坐标系的原点处，极轴与轴非负半轴重合，直线的参数方程为:

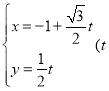    为参数）,曲线的极坐标方程为:.

    （1）写出曲线的直角坐标方程和直线的普通方程;

    （2）设直线与曲线相交于两点,求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

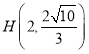    【题目】已知椭圆的右焦点为，点在椭圆上.

    （1）求椭圆的方程；

    （2）点在圆上，且在第一象限，过作的切线交椭圆于两点，问：的周长是否为定值？若是，求出定值；若不是。说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，.

    （1）令，求的单调区间；

    （2）已知在处取得极大值.求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝xln x．

    （1）求函数f（x）的极值点；

    （2）设函数g（x）＝f（x）－a（x－1），其中a∈R，求函数g（x）在区间[1，e]上的最小值．（其中e为自然对数的底数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从遂宁市中、小学生中抽取部分学生，进行肺活量调查．经了解，我市小学、初中、高中三个学段学生的肺活量有较大差异，而同一学段男女生的肺活量差异不大．在下面的抽样方法中，最合理的抽样方法是

    A. 简单的随机抽样 B. 按性别分层抽样

    C. 按学段分层抽样 D. 系统抽样

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从装有6个红球和5个白球的口袋中任取4个球，那么下列是互斥而不对立的事件是（ ）

    A. 至少一个红球与都是红球

    B. 至少一个红球与至少一个白球

    C. 至少一个红球与都是白球

    D. 恰有一个红球与恰有两个红球

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在区间上，若函数为增函数，而函数为减函数，则称函数为区间上的“弱增”函数.则下列函数中，在区间上不是“弱增”函数的为（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线l1∥l2，在l1上取3个点，在l2上取2个点，由这5个点能确定平面的个数为 ( 　)

    A. 5 B. 4 C. 9 D. 1

    查看答案和解析>>

    同步练习册答案